A moving charge experience a force in a magnetic field.
$F = Bqv \, sin \, \theta$, where
- F is force acting on a current carrying conductor
- B is magnetic flux density
- q is magnitude of charge
- v is velocity of charge
- $\theta$ is the angle the velocity makes with the magnetic field
Derivation of above equation:
Consider a positive charge q moving at constant speed v at right angles to a magnetic field of flux density B. Assuming that the charge travels a distance l in time t, its speed is $v = \frac{l}{t}$ .
The moving charge can be seen as a current of $I = \frac{q}{t}$ .
Hence, the force on the charge is given by:
$F = B I l$
$F = B \left( \frac{q}{t} \right) l$, substituting l
$F = Bqv$, substituting v
Effect of magnetic force on charge
Work done on the charged particle is always zero as F is ALWAYS perpendicular to the direction of travel(or displacement) and the distance travelled in the direction of the force is zero.
- Hence, no energy is gained or lost by the particle moving through the magnetic field and the particle’s speed is always constant.
Since the force is of constant magnitude and it always at right angles to the displacement, the conditions are met for circular motion. Hence, the magnetic force on a moving charge provides a centripetal force to the charge.
$\frac{mv^{2}}{r} = Bqv$, where m is mass of moving charge and r is radius of orbit
$B = \frac{mv}{qr}$
Making r the subject,
$r = \frac{mv}{qB}$
$r \propto v$,if charge and mass are constant.
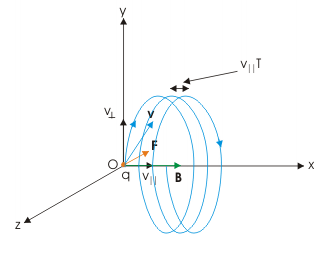
If the charged particle enters the uniform field at angles other than right angles, it will take a spiral(or helical) path as shown in the figure below.
- Reason: Component of velocity parallel to the magnetic field is unaffected by magnetic field and the particle will continue to drift along parallel to the magnetic field in addition to moving in circular motion
Image By: Singh, S.(2009, August 24).Motion of a charged particle in magnetic field. Retrieved from the Connexions Web site:http://cnx.org/content/m31345/1.9/