Table of Contents
Addition Of Forces
Since force is a vector quantity, forces can be represented by an arrow diagram.
- The magnitude of the force is represented by the length of the arrow
- The direction of the force is represented by the direction in which the arrow is pointed.
Resultant Force
Resultant force is the combination of 2 or more forces.
- The effect on a body produced by 2 or more forces acting on it will be the same as that produced by their resultant force.
- Hence, resultant force is used to simplify force diagrams – it is easier to deal with one resultant force than multiple forces.
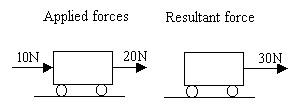
Adding Forces In Same Direction
The above figure shows two forces – 10 N and 20 N acting on a car. The resultant force will be 30 N to the right, which is obtained by adding the two forces numerically.
In the general case, where there is $F_{1}$ to $F_{n}$ acting on an object in the same direction,
$$F_{\text{resultant}} = F_{1} + F_{2} + … + F_{n}$$
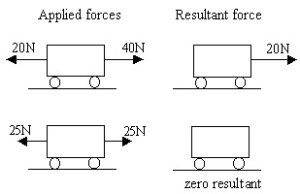
Adding Forces In Opposite Direction
When the applied forces are in the opposite direction, the resultant force is dependent on the magnitude of the forces. Using the first car in the above figure, there are two forces 20 N and 40 N acting on it. The resultant force will be 20 N as $F_{\text{resultant}} = 40 \, – 20 = 20 \, \text{N}$ to the right.
When the two forces are same in magnitude but different in direction, the resultant force will be 0 (as seen above)
Slightly More Advanced Trick Of Adding Forces
Taking rightward as positive, the forces acting on the car will be -20 N (Negative because the force is to the left) and + 40 N.
Using the addition of forces, $F_{\text{resultant}} = (\, – 20) + 40 = + 20 \, \text{N}$, which is 20 N to the right.
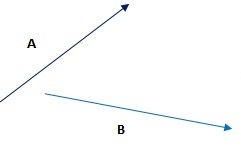
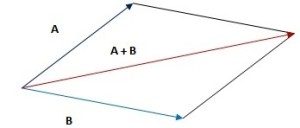
Drawing Force Diagrams Of Forces At An Angle To Each Other
This will be more complicated than the previous two cases. We can use the parallelogram law of vector addition to find the resultant force.
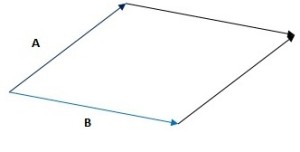
Consider the above diagram, we are given two forces – A and B. We will shift B to match up with A as seen below. Ensure that force A and B are drawn to scale (e.g. 1 cm to 5 N)
After shifting B, we draw two more lines to make it a parallelogram. The resultant force will just be the red line in the diagram below. You can measure the diagonal (A + B line) to find the resultant force.
Bonus: Can you work out what happens if the two forces are at $90^{\circ}$ to each other?
[A Level] Adding Of Force Vectors
Force is a vector. The resultant of two forces acting on the same object:
$$\vec{R} = \vec{F}_{1}+\vec{F}_{2}$$
If there are more than 2 forces acting on the same object, the resultant force is given by:
$$\begin{aligned} \vec{R} &= \vec{F}_{1} + \vec{F}_{2} + \vec{F}_{3} + \dots \\ &= \sum\limits_{i} \vec{F}_{i} \\ &= \sum \vec{F} \end{aligned}$$
Forces can be resolved into perpendicular components (see next section on how to resolve vectors):
$$\vec{R} = R_{x} \, \hat{i} + R_{y} \, \hat{j} + R_{z} \, \hat{z}$$
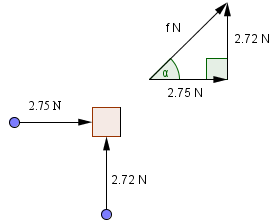
[A Level] Steps To Resolve Vectors
When combining two or more vectors, a systematic approach can be employed to ascertain the resultant vector effectively. The following steps outline the procedure:
- Coordinate System Orientation:
- Begin by selecting the orientation of the x-y coordinate system. This choice establishes the reference axes for the vector analysis.
- Origin-Point Vector Representation:
- Represent each vector by drawing them in a manner that originates from the coordinate system’s origin. This practice provides a clear starting point for vector addition.
- Vector Specification:
- Ensure each vector is distinctly labeled and accurately portrayed with the appropriate lengths and directions. This step is crucial for precise vector representation.
- Component Determination:
- Break down each vector into its x and y components. Decomposing the vectors in this way facilitates the subsequent analysis and manipulation of their individual contributions.
- Resultant Vector Components:
- Determine the resultant vector’s components along both the x-axis and y-axis by algebraically summing the respective components of all involved vectors.
- Magnitude Calculation Using Pythagoras Theorem:
- Apply the Pythagorean theorem to compute the magnitude of the resultant vector. This involves taking the square root of the sum of the squares of its x and y components.
- Angle Determination Using Trigonometry:
- Utilize trigonometric principles to ascertain the angle that the resultant vector forms with either the x-axis or the y-axis. This step provides valuable information about the direction of the resultant vector in relation to the chosen coordinate system.
By methodically following these procedures, the process of adding vectors becomes more organized and systematic, ensuring accurate determination of the resultant vector’s magnitude and direction.
Worked Examples
Example 1
Three forces of 3 N, 1.5 N and 2 N are acting on an object, as shown in the picture below.
What is the resultant due to the three forces?
Click here to show/hide answer
From the diagram above and taking rightward as positive, the resultant force is given by:
$$\begin{aligned} F_{\text{resultant}} &=3-1.5-2 \\ &=-0.5 \text{ N} \end{aligned}$$