Using a beam of molybdenum Kɑ X-ray of wavelength 0.0709 nm on a graphite target.
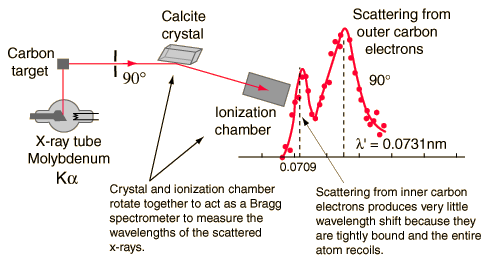 There are two peaks in the intensity of the scattered X-rays as a function of the wavelength. The difference between the two peak wavelengths is the Compton shift.
There are two peaks in the intensity of the scattered X-rays as a function of the wavelength. The difference between the two peak wavelengths is the Compton shift.
- The second peak cannot be explained by classical physics.
Solved by assuming that the incoming X-ray beam was not a wave but a collection of photons, each of energy E = hf, that collided with free electrons in the scattering target. = Photon behaving as a particle.
- Photons are not absorbed as it is too high in energy.
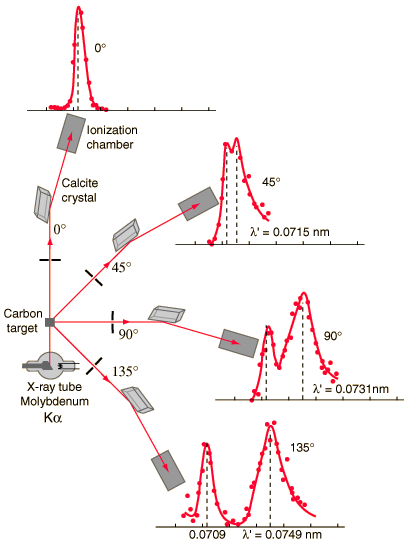 Diagram showing the experimental data obtained at various scattering angles. The Compton shift increases with increasing scattering angle, due to greater drop in energy of scattered photon.
Diagram showing the experimental data obtained at various scattering angles. The Compton shift increases with increasing scattering angle, due to greater drop in energy of scattered photon.
Compton Shift Equation: $\lambda_{f} – \lambda_{i} = \frac{h}{m_{o}c} \left( 1 – cos \, \theta \right)$
Click here for the derivation of the Compton Shift Equation.
Video of an X-ray photon colliding with an electron. (The photon is scattered and the electron is ejected from the atom):
Explanation for first peak:
A photon collides with an electron that is tightly bounded to the atom. The photon is essentially interacting with the whole atom. The mass that must be substituted into the Compton shift equation will be the mass of the atom(not the electron). Since the mass of the atom is around 22,000 times that of an electron, the Compton shift is negligible. Hence, the photon is not modified in wavelength.
Explanation for second peak:
A photon collides with an electron that is loosely bound to the atom. The photon imparts some of its energy to the electron, hence freeing the electron. The photon experience a loss in energy = decrease in frequency = increase in wavelength.