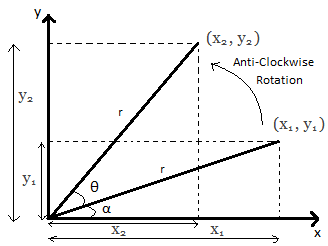
Rotation of object relative to FIXED axis:
Basic equations you can get by looking at the diagram above:
$x_{1} = r \cos {\alpha} $ $x_{2} = r \cos {(\theta + \alpha)} $
$ y_{1} = r \sin {\alpha} $ $y_{2} = r \sin {(\theta + \alpha)}$
Using the equations above:
$\begin{align} x_{2} &= r \cos {(\theta + \alpha)} \\
&= r\cos \theta \cos \alpha – r\sin \theta \sin \alpha \\
&= (r\cos \alpha) \cos \theta – (r \sin \alpha) \sin \theta \\
&= x_{1} \cos \theta – y_{1} \sin \theta
\end{align}$
$\begin{align} y_{2} &= r \sin {(\theta + \alpha)} \\
&= r\sin \theta \cos \alpha + r\cos \theta \sin \alpha \\
&= (r\cos \alpha) \cos \theta + (r \sin \alpha) \cos \theta \\
&= x_{1} \sin \theta + y_{1} \cos \theta
\end{align}$
Hence, For an anti-clockwise rotation,
$ \begin{pmatrix}
x_{2} \\
y_{2}
\end{pmatrix} = \begin{pmatrix}
\cos \theta & – \sin \theta \\
\sin \theta & \cos \theta
\end{pmatrix}\begin{pmatrix}
x_{1} \\
y_{1}
\end{pmatrix}$
$\begin{pmatrix}
\cos \theta & – \sin \theta \\
\sin \theta & \cos \theta
\end{pmatrix}$ is called the rotation matrix. Its determinant is 1.
To find the clockwise rotation matrix, you can do the calculations again. OR you can just transpose the above matrix OR you can substitute $- \theta$ into the matrix (see note below).
Hence, the clockwise rotation matrix is: $\begin{pmatrix}
\cos \theta & \sin \theta \\
-\sin \theta & \cos \theta
\end{pmatrix}$
Note: Since clockwise rotation means rotating in the anti-clockwise direction by $- \theta$, you can just substitute $- \theta$ into the anti-clockwise matrix to get the clockwise matrix. Since cos is an even function, it will not be affected by the $- \theta$. (- cos x = cos x)
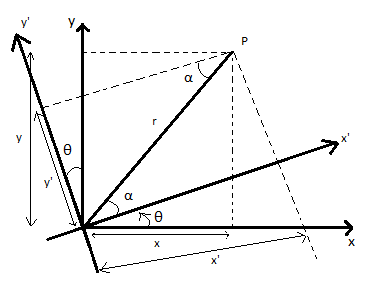
Rotation of coordinate axes:
Basic equations:
$ x’ = r \cos \alpha $ $x = r \cos (\theta + \alpha)$
$y’ = r \sin \alpha $ $y = r \sin (\theta + \alpha)$
Using the basic equations:
Equation 1: $\begin{align}x &= r\cos (\theta + \alpha) \\
&= r\cos \theta \cos \alpha – r \sin \theta \sin \alpha \\
&= x’ \cos \theta – y’ \sin \theta \end{align}$
Equation 2: $\begin{align}y &= r\sin (\theta + \alpha) \\
&= r\sin \theta \cos \alpha + r \cos \theta \sin \alpha \\
&= x’ \sin \theta + y’ \cos \theta \end{align}$
From equation 2,
$x’ = \frac{y – y’ \cos \theta}{\sin \theta}$ $y’ = \frac{y – x’ \sin \theta}{\cos \theta}$
Substitute the above 2 equations into equation 1 and you will get:
$y’ = -x \sin \theta + y\cos \theta$ $x’ = x \cos \theta + y \sin \theta$
Hence,
$ \begin{pmatrix}
x \\
y
\end{pmatrix} = \begin{pmatrix}
\cos \theta & – \sin \theta \\
\sin \theta & \cos \theta
\end{pmatrix}\begin{pmatrix}
x’ \\
y’
\end{pmatrix}$
$ \begin{pmatrix}
x’ \\
y’
\end{pmatrix} = \begin{pmatrix}
\cos \theta & \sin \theta \\
-\sin \theta & \cos \theta
\end{pmatrix}\begin{pmatrix}
x \\
y
\end{pmatrix}$