Table of Contents
Compton Shift
The Compton effect demonstrates the particle-like properties of light. When X-rays collide with an electron, they scatter with a change in wavelength (the Compton shift) that depends only on the angle of scattering, $\theta$, and not on the intensity of the X-ray. This phenomenon supports the particle theory of light, emphasizing its dual nature.
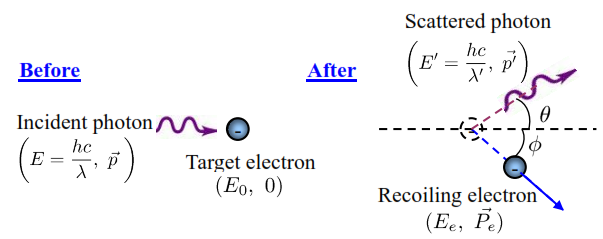
Initial Setup Of Compton Shift Equation Derivation
Using the above diagram, derive the Compton Shift Equation.
Derivation
Conservation Of Momentum
The initial momentum of the photon is given by $p$ (before collision), and after collision, the photon’s momentum is $p’$ at an angle $\theta$ to the original direction. The electron, initially at rest, gains momentum $P_e$ at an angle $\phi$. Applying the conservation of momentum in two dimensions (along and perpendicular to the initial photon direction), we get:
Along the initial direction (Horizontal in this case):
$$\begin{aligned}p \, &= p’ \, \text{cos} \, \theta + P_{e} \, \text{cos} \, \phi \\ P_{e} \, \text{cos} \, \phi \, &= p-p’ \, \text{cos} \, \theta \end{aligned} $$
Perpendicular to the initial direction (Vertical in this case):
$$\begin{aligned} 0 \, &= p’ \, \text{sin} \, \theta \, – P_{e} \, \text{sin} \, \phi \\ P_{e} \, \text{sin} \, \phi \, &= p’ \, \text{sin} \, \theta \end{aligned}$$
Deriving Intermediate Equation – Equation 1
Next, we combine these momentum conservation equations and use the trigonometric identity $\sin^2 \phi + \cos^2 \phi = 1$,
$$\begin{aligned} \sin^2 \phi + \cos^2 \phi &= 1 \\ P_{e}^{2}\sin^2 \phi + P_{e}^{2}\cos^{2} \phi &= P_{e}^{2} \\ P^{2}_{e} \, &= \left( p-p’ \, \text{cos} \, \theta \right)^{2} + p’^{2} \, \text{sin}^{2} \, \theta \\ P^{2}_{e} \, &= p^{2} + p’^{2}-2pp’ \, \text{cos} \, \theta \end{aligned}$$
$$ P^{2}_{e} \, = p^{2} + p’^{2}-2pp’ \, \text{cos} \, \theta \tag{1}$$
Conservation Of Energy
Conservation of energy for the system gives:
$$ E + E_{o} \, = E’ + E_{e} \tag{2}$$
Where $E$ and $E’$ are the energies of the photon before and after the collision, $E_0$ is the rest energy of the electron, and $E_e$ is the energy of the recoiled electron.
Next, we note that:
The relativistic energy-momentum relation for the photon is given by:
$$E = pc$$
The relativistic energy-momentum relation for the electron is given by:
$$E^{2} = m^{2} c^{4} + p^{2} c^{2}$$
We use the two relativistic energy-momentum relations in Equation 2. We will now have:
$$\begin{aligned} pc + mc^{2} \, &= p’c + \left(m^{2} c^{4} + P^{2}_{e} c^{2} \right)^{\frac{1}{2}} \\ \left(p-p’ + mc \right)^{2} \, &= m^{2}c^{2} + P^{2}_{e} \end{aligned}$$
Final Steps
Using equation 1 to get rid of $P^{2}_{e}$ in the above equation, we obtain
$$\require{cancel} \begin{aligned} \left(p-p’ + mc \right)^{2} \, &= m^{2}c^{2} + \left(p^{2} + p’^{2} – 2pp’ \, \text{cos} \, \theta \right) \\ \cancel{p^{2}} + \cancel{p’^{2}} + \cancel{m^{2}c^{2}} + 2 \left( – pp’ + pmc-p’mc \right) \, &= \cancel{m^{2}c^{2}} + \cancel{p^{2}} + \cancel{p’^{2}}-2pp’ \, \text{cos} \, \theta \\ pmc-p’mc \, &= pp’ \left( 1-\text{cos} \, \theta \right) \\ \frac{mc}{p’}-\frac{mc}{p} \, &= 1-\text{cos} \, \theta \\ \frac{mc \lambda’}{h}-\frac{mc \lambda}{h} \, &= 1-\text{cos} \, \theta \\ \lambda’-\lambda \, &= \frac{h}{mc} \left( 1-\text{cos} \, \theta \right) \end{aligned}$$
We’re done!
This equation highlights the quantum nature of light, showing that the change in wavelength ($\lambda’ – \lambda$) depends only on the scattering angle $\theta$ and the Planck constant $h$, with $m$ being the electron’s rest mass and $c$ the speed of light. This result is a cornerstone in quantum mechanics, demonstrating the quantized interaction between electromagnetic radiation and matter.