Table of Contents
Distance
Distance travelled by an object is the length of path taken.
- SI unit is metre (m)
- Scalar quantity
- Can never be negative and distance travelled will never decrease
Displacement
Displacement is the shortest distance from the initial to the final position of an object.
- SI unit is metre (m)
- Vector quantity
- Positive Displacement: Occurs when an object moves in the positive direction (e.g., forward or right).
- Negative Displacement: Occurs when an object moves in the negative direction (e.g., backward or left).
Distinguishing Between Distance & Displacement
If you have problems grasping the difference in concept of displacement and distance travelled, please study the example below.
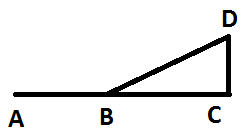
Consider the diagram above:
Difference between distance and displacement: If an object started travelling from B to C and ends at D, distance travelled is BC + CD. Displacement is BD.
Displacement can be ZERO: If the object started travelling from B to C to D and ends at B, distance travelled is BC + CD + DB. Displacement is ZERO. (The object ends at the same place it started)
Displacement can be NEGATIVE: If the object travels from B to A, the displacement is negative. By CONVENTION, the direction towards the right and top are positive. A way to remember: Go right = positive, go left = negative.
Table Showing Differences Between Distance & Displacement
| Distance | Displacement |
|---|---|
| The total length covered by a moving object regardless of the direction of motion | The distance measured in a straight line from a fixed reference point |
| Has magnitude only | Has both magnitude and direction |
| SI unit: metre ($m$) | SI unit: metre ($m$) |
Worked Examples
Example 1
Ali walked 1 km to the North, then 1 km to the East and followed by 1 km to the South. What is the distance covered by Ali? What is his final displacement?
Show/Hide Answer
Distance: $1 + 1 + 1 = 3 \, \text{km}$
Displacement: 1 km east of starting point.
Example 2
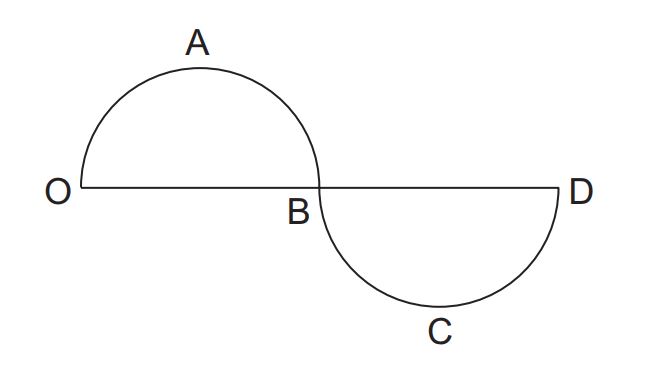
A car travelled from point O to D along the curved path OABCD. What is (a) the distance travelled by the car, and (b) the displacement of the car?
Show/Hide Answer
The distance travelled by the car is OABCD.
The displacement of the car from point O is OD (to the right of O).
Example 3
Can the magnitude of particle’s displacement be greater than the distance traveled? Explain.
Show/Hide Answer
No, the magnitude of the displacement is always less than or equal to the distance travelled.
If two displacements in the same direction are added, then the magnitude of their sum will be equal to the distance travelled. Two vectors in any other orientation will give a displacement less than the distance travelled. If you first walk 3 metres east, and then 4 metres south, you will have walked a total distance of 7 metres, but you will only be 5 metres from your starting point.
Example 4
A book is moved once around the perimeter of a tabletop with the dimensions 1.0 m X 2.0 m. If the book ends up at its initial position, what is its displacement? What is the distance travelled?
Show/Hide Answer
The book’s displacement is zero, as it ends up at the point from which it started. The distance travelled is 6.0 metres.