Table of Contents
Electric Current: Overview
Electric current is the movement of electric charges and is fundamental to understanding current electricity. This phenomenon is distinct from static electricity, also known as electrostatics, where charges remain stationary.
Definition
Electric current, denoted as $I$, is the rate of flow of charges $Q$ through a particular cross sectional area with respect to time.. It is measured in amperes $A$, a standard unit. To measure electric current accurately, an ammeter is used, which must be connected in series with the circuit. The formula $I = \frac{Q}{t}$ mathematically defines the relationship between current, charge, and time, indicating that a current of one ampere equals a charge flow of one coulomb per second (1 $A$ = 1 $C \, S^{-1}$).
$$\begin{aligned} I &= \frac{\text{amount of charge flowing}}{\text{time to flow}} \\ &= \frac{Q}{t} \\ &= \text{or } \frac{\Delta Q}{\Delta t} \end{aligned}$$
, where
- I = current (in $\text{A}$),
- Q = charge (in $\text{C}$),
- t = time (in $\text{s}$)
Measurement of Electric Currents
To measure electric currents accurately, an ammeter is the instrument of choice. For effective measurement, it is crucial to connect the ammeter in series within the circuit. Specifically, the positive terminal of the ammeter should align with the positive terminal of the power supply.
A basic moving coil ammeter is designed to measure direct current (DC) and displays the readings on an analog interface. This type of ammeter might offer dual ranges, allowing for readings across two different scales.
Alternatively, a multimeter, which can feature either a digital or analog display extends the capability to measure both alternating (AC) and direct (DC) currents. This versatility also includes the measurement of voltages and resistance. To use a multimeter, the user must first select the desired measurement function, such as DC current.
When conducting measurements with any ammeter, selecting an appropriate range is vital to ensure accuracy. For instance, when expecting a current in the milliamp range, one might choose the 10 mA setting and read the current value directly from the display. If the initial reading exceeds the scale, adjusting to a higher range, like 100 mA, reduces the sensitivity and accommodates larger currents, ensuring precise measurements.
Charge Carriers and Current Direction
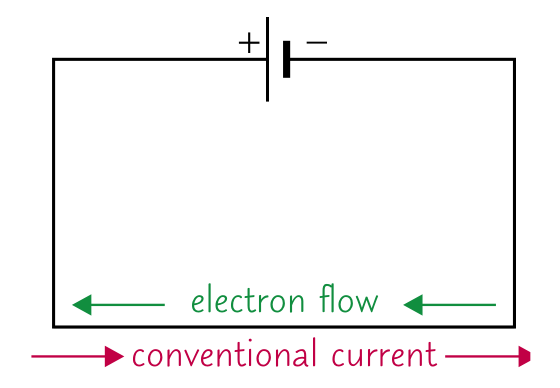
Within a circuit, electrons (which are negatively charged) move from a battery’s negative terminal to its positive terminal. The movement of this charge is referred to as electric current.
Alternatively, one can conceptualize current as the flow of positive charge in the opposite direction, moving from positive to negative, known as conventional current. Hence, the conventional current direction is the direction in which positive charges effectively move.
In metal conductors (solids), it is the negative charge that flows and hence the conventional current and the negative charge(electrons) flow in opposite direction.
In gases and liquids, electric current typically involves positive ions moving in one direction and negative ions moving in the opposite direction.
Current In The Form Of Charged Ions
Electric currents are not exclusively characterized by the movement of electrons. Charged ions in a solution, referred to as an electrolyte, can also contribute to current flow.
For instance, in car batteries, the flow of hydrogen (H+) ions and sulfate ($SO_{4}^{2-}$) ions is instrumental, capable of producing currents reaching up to 450 A for a duration of 2.5 seconds.
The current is a result of the collective contribution of both ions in the solution. Its measurement externally is achievable through an ammeter connected in series with both electrodes.
Magnetic Field Generation
A key characteristic of electric current is its ability to generate a magnetic field. The strength of this magnetic field correlates with the magnitude of the electric current.
Types of Electric Current
Electric current can be classified into two main types based on its flow direction:
- Direct Current (DC): The flow of electric charge in a constant direction.
- Alternating Current (AC): The direction of electric charge flow periodically reverses.
Analogy to a River
To aid in understanding electric current, one can draw an analogy to a river. Just as water flows through a river, electric current signifies the flow of electric charge through a circuit. This analogy is helpful for visualizing the continuous movement and directionality of electric current, similar to water’s journey through a river system.
[A Level] Instantaneous Current
$$I = \frac{dQ}{dt}$$
The charge that passes through a given point is the product of the steady current flowing past the point and the time during which the current flows.
- Unit of charge: coulomb (C)
- One coulomb is the quantity of charge that flows through a point when a steady current of one ampere flows for one second.
Worked Examples
Example 1
An electric current in a wire involves the movement of
- electrons
- atoms
- molecules
- protons
Show/Hide Answer
A. Electric current in a wire (solid conductor) involves the movement of electrons.
Example 2
The lower part of a cloud has a positive charge. The cloud discharges in a flash of lightning. In which direction do electrons and conventional current flow?
Show/Hide Answer
As the cloud is positively charged, negative charges (electrons) flow upwards. Therefore, the conventional current flow is in the opposite direction (downwards).
Example 3
A battery moves a charge of 60 C around a circuit at a constant rate in a time of 20 s. What is the current in the circuit?
Show/Hide Answer
Current is the rate of movement of charge.
$$\begin{aligned} I &= \frac{Q}{t} \\ &= \frac{60}{20} \\ &= 3.0 \, C/s \\ &= 3.0 \, A \end{aligned}$$
Example 4
Describe the process by which electrical conduction happens within a metal.
Show/Hide Answer
Electrical conduction in metals occurs when electrons move freely throughout the metal’s lattice structure. In metals, the outer electrons of atoms are not tightly bound to their parent atoms but are instead free to move within the material. This sea of delocalized electrons allows metals to conduct electric current efficiently. When an electric field is applied across a metal, these free electrons drift towards the positive electrode, creating a flow of electric charge that we observe as electrical conduction.
Example 5
Describe the procedure for connecting an ammeter to a circuit.
Show/Hide Answer
To integrate an ammeter into a circuit for measuring current, it is essential to connect it in series with the circuit components. This setup ensures that all the current flowing through the circuit also passes through the ammeter. The correct orientation is crucial; the positive terminal of the ammeter should be connected to the positive side of the power source. This alignment allows the ammeter to accurately measure the current flow without interfering with the circuit’s operation.
Example 6
600 C of charge passes a point in a circuit in 30 seconds. What is the current at that point?
Click here to show/hide answer
$$\begin{aligned} I &= \frac{Q}{t} \\ &= \frac{600}{30} \\ &= 20 \text{ A} \end{aligned}$$
Example 7
How long does it take to transfer 24 C of charge if the average current is 4 A?
Click here to show/hide answer
$$\begin{aligned} t &= \frac{Q}{I} \\ &= \frac{24}{4} \\ &= 6 \text{ s} \end{aligned}$$