The probability that an electron energy state will be occupied at a particular temperature T is given by the Fermi function f(E).
$$f (E) = \frac{1}{ e^{\frac{E \, – E_{F}}{kT}} + 1}$$
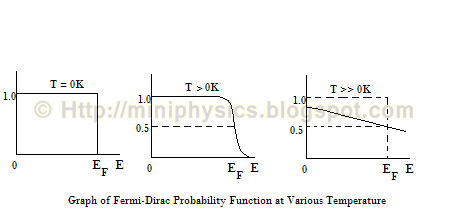
The basic nature of this function dictates that at ordinary temperatures, nmost of the levels up to the Fermi Level EF are filled, and relatively few electrons have energies above the Fermi Level. The Fermi level is on the order of electron volts (e.g. 7eV for copper), whereas the thermal energy kT is only about 0.026 eV at 300 K. If you put those numbers into the Fermi function at ordinary temperatures, you will find that its value is essentially 1 up to the Fermi level, and rapidly approaches zero above it.
Note that for any temperature T, when E = EF, there is a 50% chance of the state being occupied as f(E) = 0.50.
Multiplying the density of states g(E), to the Fermi function, f(E), we will obtain the density of occupied states, N(E).
N(E) = f(E) g(E)
More specifically, the density of occupied states between E and E + dE is given by N(E)dE.
Integrating N(E)dE from E = 0 to E = infinity, we will obtain the electron density, n.
$$\begin{aligned} n \, &= \int\limits^{\infty}_{0} N (E) \, dE \\ n \, &= \int\limits^{\infty}_{0} f(E) g(E) \, dE \end{aligned}$$
Back To Solid State Physics