Table of Contents
Force On A Current-carrying Conductor
When current-carrying conductor is placed in a magnetic field, it will experience a force when the magnetic field direction is not parallel to the current direction. The magnitude of the force is maximum when the magnetic field and current directions are mutually perpendicular to each other. The force decreases when the angle between the magnetic field and current directions is smaller than $90^{\circ}$.
Factors Affecting Magnetic Force On A Current-carrying Conductor In A Magnetic Field:
- Angle between the magnetic field and current directions (More about this below)
- Magnetic field strength (Stronger magnetic field $\rightarrow$ stronger force)
- Amount of current in conductor (Higher current $\rightarrow$ stronger force)
- Length of conductor within magnetic field (Longer conductor $\rightarrow$ stronger force)
If the current direction is PARALLEL to the magnetic field, there will NO force on the conductor by the magnetic field. The magnitude of the force is MAXIMUM when the angle between the magnetic field and current direction is $90^{\circ}$.
This is commonly exploited to produce a turning effect in a current-carrying coil to produce an electric motor.
It does not have to be a current carrying conductor to experience a force due to the magnetic field. The magnetic field actually interacts with the moving electrons in the conductor to produce the force. Hence, electrons that are moving in the direction perpendicular to the magnetic field will experience the force as well. This means that if you pass an electron beam through a magnetic field, it will be deflected. (provided it is perpendicular)
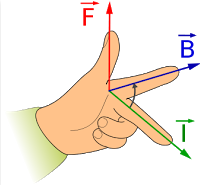
Fleming’s Left-hand Rule – Direction Of The Force
When a conductor carrying a current is placed in a magnetic field, the conductor experiences a magnetic force.
- The direction of this force is always right angles to the plane containing both the conductor and the magnetic field, and is predicted by Fleming’s Left-Hand Rule.
- F is Force, B is Magnetic field, I is current.
- From the name of the rule, use your left hand.
E.g. If current flowing towards to right and the magnetic field is pointing into the paper, the direction of the force is predicted by the Fleming’s left hand rule to be upwards.
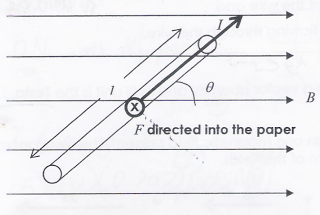
Formula For Magnetic Force On A Current-carrying Conductor In A Magnetic Field (A Level)
Referring to the diagram above, F is Force, B is Magnetic field, I is current.
$F = B I l \, sin \, \theta$, where
- F is force acting on a current carrying conductor,B is magnetic flux density (magnetic field strength),
- I is magnitude of current flowing through the conductor,
- $l$ is length of conductor,
- $\theta$ is angle that conductor makes with the magnetic field.
When the conductor is perpendicular to the magnetic field, the force will be maximum. When it is parallel to the magnetic field, the force will be zero.
Kyamafi
Mnazingua