Table of Contents
Introduction
Materials can be identified by the characteristics they display under the influence of applied forces. Various materials exhibit distinct properties, and scientists assess them by subjecting them to compressive or tensile forces.
In 1678, Robert Hooke documented his findings on elasticity, noting that certain springs exhibited a linear region of extension corresponding to the applied force. This insight from his investigations into springs led to the creation of a spring for the initial portable timepiece, now known as a watch. Hooke observed that the extension of these springs was proportional to the applied force within a specific range, which became known as the Hooke’s Law.
Compressive & Tensile Forces
When you apply a force to an object you can cause it to stretch and deform (change shape).
- Compressive forces refer to those exerted on an object with the intent of compressing or reducing its size along the direction of the applied forces. For instance, placing a substantial weight on a column, combined with the upward force at the bottom, will result in a decrease in the column’s height.
- Tensile forces are forces that aim to pull or elongate an object. An illustration of this is the metal ropes supporting an elevator, which experience tensile forces from the weight of the lift and the upward pull exerted by the ceiling on the rope’s end.
Elastic Objects
Elastic objects are objects that return to their original shape after this deforming force is removed, e.g. springs.
- A material is considered elastic if it reverts to its initial dimensions upon the removal of the applied load.
- On the other hand, a material is deemed plastic if it undergoes permanent deformation and fails to return to its original dimensions after the applied load is removed.
When a spring is supported at the top and a weight is attached to the bottom, it stretches.
Hooke’s Law
Hooke’s law establishes a linear relationship between the force applied to a spring or elastic material and the resulting deformation or change in length (extension).
Mathematically expressed as:
$$F = k \Delta x$$
, where
- $F$ is the force applied (in $N),
- $k$ is the spring constant (a measure of stiffness) (in $\text{N m}^{-1}$), and
- Δx represents the displacement from the material’s equilibrium position (in $m$).
Hooke’s Law holds true within the elastic limit of a material.
- Elastic limit is the load above which a material is permanently deformed.
- This means that as long as the force applied does not exceed the material’s elastic limit, the resulting deformation is directly proportional to the force, reflecting the material’s ability to return to its original shape once the force is removed.
- Hooke’s Law serves as a cornerstone in understanding the mechanical behavior of materials and plays a crucial role in various scientific and engineering applications.
Spring Constant
The spring constant, denoted as $k$, quantifies the resistance of a spring to bending or stretching. A higher spring constant indicates greater stiffness in the spring.
- SI unit of $k$: $\text{N m}^{-1}$
- $\uparrow$ k( Higher stiffness), $\downarrow$ extension
- Applies to springs, elastic springs and metals in form of wires
Limit Of Proportionality
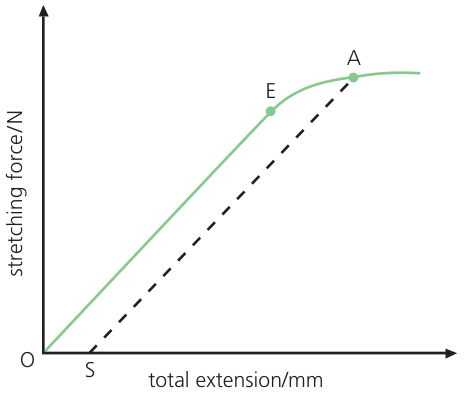
The limit of proportionality is a crucial parameter in the study of material behavior under stress and strain. It represents the maximum stress level at which the deformation of a material remains directly proportional to the applied stress. In other words, as long as the applied stress does not exceed the limit of proportionality, the material will return to its original shape once the stress is removed, following Hooke’s Law. This phase is characteristic of the material’s elastic behavior, wherein the response to stress is linear.
Beyond the limit of proportionality, a material enters the elastic limit ($E$), where the relationship between stress and strain becomes non-linear, and the material undergoes permanent deformation. This transition marks the point at which the elastic limit is surpassed, and the material no longer follows Hooke’s Law. Engineers and scientists use the limit of proportionality to assess the safe operating range of materials in various applications, ensuring that structures and components can endure stress without undergoing irreversible deformation or failure.
Understanding the limit of proportionality is essential for designing materials and structures that can withstand different loads while maintaining their integrity. It is a critical factor in determining the reliability and safety of various engineering components, guiding the selection of materials for specific applications based on their elastic properties and performance under stress.
Effective Spring Constant
Springs connected in parallel
$k_{eff} \, = \, k_{1} + k_{2} + \, …$
Springs connected in series
$\frac{1}{k_{eff}} = \frac{1}{k_{1}} + \frac{1}{k_{2}} + \, …$
- Same load, less extension compared to series
Elastic Potential Energy (or Elastic Strain Energy)
Elastic potential energy, also referred to as elastic strain energy, is a form of mechanical energy stored within a material when it undergoes deformation due to an applied force. This type of energy is particularly associated with elastic materials, such as springs or rubber bands, which have the ability to return to their original shape after the force is removed. When these materials are stretched or compressed, they store potential energy in the form of the work done on them. The magnitude of the elastic potential energy is directly proportional to the amount of deformation and the material’s elastic constant, known as the spring constant.
The mathematical expression for elastic potential energy $W$ in a spring system is given by Hooke’s Law:
$$W = \frac{1}{2} k_{eff} X^{2}$$
where:
- $W$ is the elastic potential energy or work done stretching the spring system,
- $k$ is the spring constant, and
- $X$ is the displacement from the equilibrium position.
This formula reflects the quadratic relationship between the displacement and the stored energy, emphasizing that the potential energy increases with the square of the displacement. Understanding and harnessing elastic potential energy play a crucial role in various engineering applications, ranging from designing shock absorbers and resilient materials to creating efficient storage systems for renewable energy.
[A Level] Young’s Modulus
Young’s Modulus, also known as the modulus of elasticity, is a fundamental material property that characterizes the stiffness or rigidity of a material under the influence of tensile or compressive forces. It is denoted by the symbol ‘$E$’ and is defined as the ratio of tensile stress to tensile strain within the elastic deformation region. In other words, Young’s Modulus represents the material’s ability to resist deformation when subjected to an applied force.
Tensile stress ($\sigma$) is the force applied per unit area, and it is calculated using the formula:
$$\sigma = \frac{F}{A}$$
where ‘F’ is the applied force and ‘A’ is the cross-sectional area of the material.
Tensile strain ($\varepsilon$) is the ratio of the change in length $\Delta L$ to the original length $L_0$, expressed as:
$$\varepsilon = \frac{\Delta L}{L_0}$$
Young’s Modulus is then defined as the ratio of tensile stress to tensile strain, given by the equation:
$$E = \frac{\sigma}{\varepsilon}$$
Understanding Young’s Modulus is crucial for assessing how a material will respond to applied forces, particularly in situations involving stretching or compressing. The higher the Young’s Modulus, the stiffer the material, indicating its ability to withstand deformation under stress. This modulus is applicable within the elastic limit of a material, beyond which permanent deformation or failure may occur.
The significance of Young’s Modulus extends beyond its mathematical formulation. For instance, in structural engineering, materials with high Young’s Modulus values are preferred for applications where rigidity and minimal deformation are critical, such as in the construction of bridges and skyscrapers. Conversely, materials with lower Young’s Modulus may be desirable in situations where flexibility and elasticity are paramount, as seen in the design of springs or shock-absorbing components. Overall, Young’s Modulus serves as a fundamental parameter in material science and engineering, providing insights into a material’s mechanical behavior under different loading conditions.
Worked Example
Example 1
What is the magnitude of the force exerted on a spring with a spring constant of $65.0 \text{N m}^{–1}$ when the spring undergoes a 12.3 cm extension?
Click here to show/hide answer
Hooke’s Law is expressed as:
$$F = -k \Delta x$$
Now, substitute the values into Hooke’s Law:
$$\begin{aligned} F &= 65.0 \, \text{N m}^{-1} \times 0.123 \, \text{m} \\ &= 8.00 \text{ N} \end{aligned}$$
Example 2
How far does a vertical spring stretch when a bag of flour weighing 7.10 kg is connected to its bottom? The spring has a spring constant of $85.0 \text{ N m}^{–1}$, and its upper end is held in place.
Click here to show/hide answer
To find how far the vertical spring stretches, we can use Hooke’s Law:
$$F = -k \Delta x$$
The force applied $F$ can be determined by the weight of the flour, which is equal to the mass $m$ times the acceleration due to gravity $g$:
$$\begin{aligned} F &= m \times g \\ &= 7.10 \times 9.81 \\ &= 69.651 \text{ N} \end{aligned}$$
Using Hooke’s Law,
$$\begin{aligned} \Delta x &= \frac{F}{k} \\ &= \frac{69.651}{85} \\ &= 0.819 \text{ m} \end{aligned}$$
Example 3
A spring A of force constant 6.0 Nm-1 is connected in series with a spring B of force constant 3.0 Nm-1. One end of the combination is securely anchored and a force of 0.60 N is applied to the other end.
(a) By how much does each spring extend?
(b) What is the force constant of the combination?
(c) What is the total elastic potential energy stored in the system?
Click here to show/hide answer
(a)
$$\begin{aligned} F &= K_a x_a \\ 0.6 &= 6(x_a) \\ \text{Extension for spring a, } x_a &= 0.100 \, \text{ m} \end{aligned}$$
$$\begin{aligned} F &= k_b x_b \\ 0.6 &= 3(x_b) \\ \text{Extension for spring b, } x_b &= 0.200 \, \text{ m} \end{aligned}$$
(b)
$$ \begin{aligned} \text{Total Extension} &= 0.10 + 0.20 \\ &= 0.300 \, \text{ m} \end{aligned}$$
$$\begin{aligned} F &= kx \\ 0.6 &= k(0.3) \\ k &= 2 \, \text{ N m}^{-1} \end{aligned}$$
]
(c)
$$\begin{aligned} \text{Total elastic P.E. stored} &= \frac{1}{2} k_{\text{eff}} x^2 \\ &= \frac{1}{2}(2)(0.3)^2 \\ &= 0.090 \, \text{J} \end{aligned}$$
Example 4
A string supports a solid iron object of mass 0.180 kg totally immersed in a liquid of density 800 kg m-3. If the density of iron is 8000 kg m-3, calculate:
(a) the upthrust acting on the object;
(b) the tension in the string
Click here to show/hide answer
(a)
$$\begin{aligned} \text{Upthrust} &= V\rho g \\ &= \left(\frac{0.180}{8000}\right)(800)(9.81) &= 0.177 \, \text{N} \end{aligned}$$
(b)
$$\begin{aligned} \text{Tension} &= (0.180)(9.81) – 0.177 \\ &= 1.59 \, \text{N} \end{aligned}$$