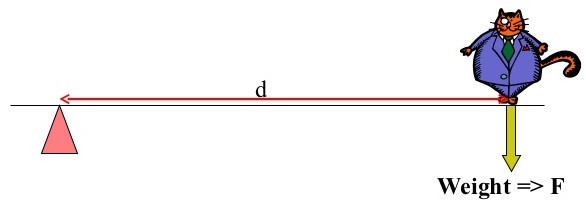Table of Contents
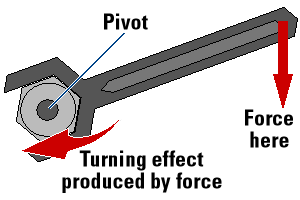
Turning Effect
If a body under the action of a net external force is allowed to rotate about a pivot, the body will tend to turn in the direction of the applied force.
Examples Of Turning Effect Of Force
- A person pushing a swing will make the swing rotate about its pivot.
- A worker applies a force to a spanner to rotate a nut.
- A person removes a bottle’s cork by pushing down the bottle opener’s lever.
- A force is applied to a door knob and the door swings open about its hinge.
- A driver can turn a steering wheel by applying a force on its rim.
Moment Of A Force
The principle of moment finds its most illustrative example in a basic lever, which consists of a rigid bar resting on a pivot or fulcrum. This simple mechanical device is employed to transfer a force into movement, effectively enabling the manipulation of a load.
The moment of a force or torque, r is defined as the turning effect of the force about a pivot and is the product of the force (F) and the perpendicular distance (d) from the line of action of the force to the pivot.
- SI unit of moment of a force is Newton-metre (Nm).
- It is a vector quantity.
- Its direction is given by the right-hand grip rule perpendicular to the plane of the force and pivot point which is parallel to the axis of rotation.
- The turning effect of the force (or moment of a force or torque) is proportional to:
- the perpendicular distance from the line of action of the force to the pivot
- the magnitude of the force
- A clockwise rotation about the pivot is a clockwise moment.
- An anticlockwise rotation about the pivot is an anticlockwise moment.
$$r = F \times d$$
,where
r is the moment of force/torque
F is the force
d is the perpendicular distance from the line of action of the force to the pivot
In order to create a moment of force, the line of action of the force must not pass through the pivot. As in this case, the $d$ will be 0 and hence, moment will be 0 as well.
Couple
A couple is a pair of forces, equal in magnitude but opposite in direction, whose lines of motion do not coincide.
- Will still rotate as there is a net moment
- As forces are equal and opposite, resultant force is zero and so there is no linear acceleration
- $r = F \times d$
Torque(Moment of a couple) is the product of one of the forces and the perpendicular distance between their lines of action of the forces.
- Can take moment from any point
Worked Examples
Example 1
Consider the figure above. Given that the cat weighs 150 N and the distance from the cat to the pivot is 30 cm, calculate the moment of force about the pivot.
Click here to show/hide answer
$$\begin{aligned} r &= F \times d \\ &= 150 \times 0.30 \\ &= 45 \text{ N m} \end{aligned}$$
Example 2
Why is it easier to open the lid of a container with a spoon than a coin?
Click here to show/hide answer
A spoon is longer than a coin. If you use them to open the lid of a container by pivoting, the perpendicular distance $d$ will be longer for a spoon than a coin.
Let’s assume that it takes an $x \text{ Nm}$ of moment of a force to open the lid and that $d_{\text{spoon}} = 2 d_{\text{coin}}$.
Find amount of force needed to open the lid if we use a spoon:
$$\begin{aligned} r &= F \times d \\ x &= F_{\text{spoon}} \times d_{\text{spoon}} \\ F_{\text{spoon}} &= \frac{x}{d_{\text{spoon}}} \end{aligned}$$
Find amount of force needed to open the lid if we use a coin:
$$\begin{aligned} r &= F \times d \\ x &= F_{\text{coin}} \times d_{\text{coin}} \\ F_{\text{coin}} &= \frac{x}{d_{\text{coin}}} \end{aligned}$$
Since $d_{\text{spoon}} = 2 d_{\text{coin}}$,
$$\begin{aligned} F_{\text{coin}} &= \frac{x}{\frac{d_{\text{spoon}}}{2}} \\ &= 2 \frac{x}{d_{\text{spoon}}} \\ &= 2 F_{\text{spoon}} \end{aligned}$$
From the calculations above ($F_{\text{coin}} = 2 F_{\text{spoon}}$), you will need twice as much force to open the lid of a container if you use a coin.