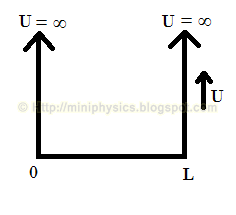
Let us now try to solve the Schrodinger equation for a particle in a one-dimensional box of width L.
Consider the walls to be infinitely high, hence U(x) = ∞ for x = 0 and x = L. Since potential energy is constant within the box, it is convenient to choose U(x) = 0 as its value. Hence for 0 < x < L,
$\frac{d^{2} \psi}{dx^{2}} = \frac{2m E}{\hbar^{2}} \psi = – k^{2} \psi$
where $k = \frac{\sqrt{2mE}}{\hbar}$ .
Note: $\hbar$ is the reduced Planck’s constant (h-bar).
Because the walls are infinitely high, the particle is bound in the box and cannot exist outside the interval 0 < x < L. Hence U(x) = 0 outside the box and at the walls. One solution that meets the boundary conditions ψ = 0 at x = 0 and x = L is
$\psi \left( x \right) = A sin \, \left( kx \right)$
At x = 0, ψ(0) = Asin 0 = 0.
At x = :, ψ(L) = Asin (kL). In order to satisfy that ψ(L) = 0, we require kL to be an integer multiple of π (kL = nπ, where n is an integer) – So that sin π = 0. Hence,
$kL = \frac{ \sqrt{2mE}}{\hbar} L = n \pi$
Solving for the allowed energies E gives
$E_{n} = \frac{n^{2} \pi^{2} \hbar^{2}}{2mL^{2}} = \frac{n^{2} h^{2}}{8mL^{2}}$
The allowed wave functions are given by
$\psi_{n} \left( x \right) = A sin \left( \frac{n \pi x}{L} \right)$
The normalisation constant A for this solution is equal to $\sqrt{\frac{2}{L}}$.