Consider now a particle in a well, but now the walls are of finite height (instead of infinitely high), which we call a potential well. If we again choose U = 0 for 0 < x < L, then U will have a finite value for x = 0 and x = L.
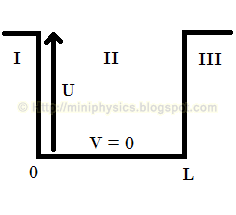 If the total energy E of the particle is less than U, then classically the particle is permanently bounded in the potential well. However, according to quantum mechanics, there is a finite possibility that the particle can be found outside the well even if E < U. This means that the wave function ψ(x) is generally non-zero outside the well (i.e. in regions I and III), which implies that the probability density |ψ|2 is also non-zero in these regions.
If the total energy E of the particle is less than U, then classically the particle is permanently bounded in the potential well. However, according to quantum mechanics, there is a finite possibility that the particle can be found outside the well even if E < U. This means that the wave function ψ(x) is generally non-zero outside the well (i.e. in regions I and III), which implies that the probability density |ψ|2 is also non-zero in these regions.
In region II where we choose U = 0, the allowed wave functions are again sinusoidal (because it is similar to the particle in a well of infinite well). However, the boundary conditions no longer require ψ(x) = 0 at x = 0 and x = L.
The Schrodinger equation for regions I and III may be written as
$\frac{d^{2} \psi}{dx^{2}} = \frac{2m \left( U – E \right)}{\hbar^{2}} \psi$
Since E < U, the coefficient on the right-hand side is positive. We can then write the equation as
$\frac{d^{2} \psi}{dx^{2}} = k^{2} \psi$
where $k^{2} = \frac{2m \left( U – E \right)}{\hbar^{2}}$ is a positive constant in regions I and III.
The general solution to the above equation is
$\psi = A e^{kx} + B e^{-kx}$
where A and B are constants.
The general solution can be used as a starting point for determining the appropriate solution for regions I and III.
In region I where x < 0, we must rule out the term Be-kx. (the term will be bigger than 1)
In region II where x > L, we must rule out the term Aekx.
Hence, the solution for region II is sinusoidal and has the form
$\psi_{II} \left( x \right) = C sin \left( kx \right) + D cos \left( kx \right)$
where C and D are constants.
These results show that the wave function decays exponentially with distance outside the potential well. In order to evaluate the complete wave function, we need to apply these conditions:
$\psi_{I} = \psi_{II}$ and $\frac{d \psi_{I}}{dx} = \frac{d \psi_{II}}{dx}$ at x = 0.
$\psi_{II} = \psi_{III}$ and $\frac{d \psi_{II}}{dx} = \frac{d \psi_{III}}{dx}$ at x = L.