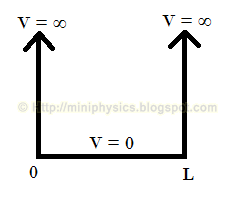
Consider a particle (e.g. an electron) that is confined to a “1-dimensional box” of length L. A 1-dimensional box is taken to be one in which its potential energy V = ∞ outside the box. Inside the box, no force acts on the particle and so its potential energy is constant which can be fixed arbitrary to be zero, ie V = 0 within the box. Thus the potential energy curve for such a particle in this box is:
Physically, V = ∞ is set so that there is no chance that the particle can penetrate the edges of the box. In quantum mechanics, particles are described by wave functions. This means that the wave function ψ associated with the particle must be exactly zero towards the ends of the box and everywhere else outside the box where V = ∞, giving zero probability of finding the particle beyond the edges of the box.
Hence, if the particle is truly confined to the box, the matter wave associated with the particle must have nodes at the end of the box, exactly just like the standing (or stationary) wave that is formed in a length of stretched string.
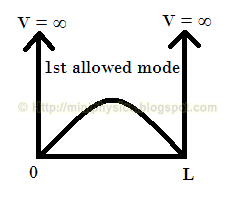
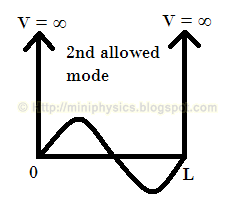
Therefore, the allowed modes of the standing wave formed must be such that the length L of the box is equal to an integer number of half-wavelengths,
$$L= n \frac{\lambda_{n}}{2}$$
, where
n = any positive integer
λ = de Broglie wavelength of the particle.
For example, the allowed modes of the standing wave formed are as shown below: