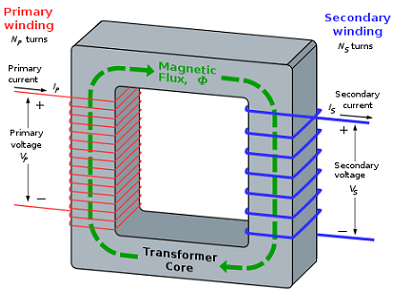
Summary:
- When an alternating voltage Vp is applied to the primary coil, an a.c. current flows in the primary coil.
- This a.c. current sets up a changing magnetic field in the iron core. The flux through the primary coil is linked to the flux in the secondary coil through the iron core.
- This alternating magnetic field induces an e.m.f. in both the coils. (See Below)
- The output voltage in the secondary coil Vs will give rise to an a.c. current in the coil itself. Thus, electrical energy can be delivered to any devise at the output.
- Since there is no flux leakage, the rate of flux change $\frac{d \phi}{dt}$ at the primary coil and the secondary coil must be the same. Since, $\frac{V_{s}}{V_{p}} = \frac{\epsilon_{s}}{\epsilon_{p}}$, $\frac{V_{s}}{V_{p}} = \frac{- N_{s} \frac{d \phi}{dt}}{- N_{p} \frac{d \phi}{dt}} = \frac{N_{s}}{N_{p}}$.
- In addition, an ideal transformer is 100% efficient. Hence, power output from the secondary coil = power supplied to the primary coil. $V_{s} l_{s} \, = \, V_{p} l_{p}$
Note: Transformer works by the principle of magnetic induction. When an a.c. flows through the primary coil, it sets up a changing flux which in turn induces an e.m.f.
Detailed Walkthrough Of The E.M.F. Induced In Both Coils:
At the primary coil:
The changing magnetic field induces an e.m.f. Ep in the primary coil (due to self-inductance) This induced e.m.f. opposes the applied voltage, Vp
$V_{p} – \mid E_{p} \mid = I_{p} r_{p}$, where
- $r_{p}$ = the primary coil resistance
- $I_{p}$ = the current in the primary coil
Induced e.m.f., Ep(due to self-inductance) = $- \, \frac{d \left( N_{p} \phi \right) }{dt} = \, – \, N_{p} \frac{d \phi}{dt}$, where
- $N_{p}$ = the number of turns in the primary coil,
- $\phi$ = the magnetic flux in the iron core linking the coils
- $\frac{d \phi}{dt}$ = the rate of change of magnetic flux in the iron core.
For an ideal transformer, rp = 0, hence $V_{p} = \mid E_{p} \mid $
At the secondary coil,
When connected to a load, the output voltage Vs (Secondary voltage) is given by:
$V_{s} = \mid E_{s} \mid – I_{s} r_{s}$,where
- $r_{s}$ = the secondary coil resistance,
- $I_{s}$ = the current in the secondary coil
Induced e.m.f. in the secondary coil, Es (through mutual induction) = $- \, \frac{d \left( N_{S} \phi \right)}{dt} = N_{S} \frac{d \phi}{dt}$, where
- $N_{s}$ = the number of turns in the secondary coil,
- $\phi$ = the magnetic flux in the iron core linking the coils
- $\frac{d \phi}{dt}$ = the rate of change of magnetic flux in the iron core.
For an ideal transformer, rs = 0, hence Vs = |Es|
Important:
$\frac{N_{s}}{N_{p}} = \frac{V_{s}}{V_{p}} = \frac{I_{p}}{I_{s}}$
For step-up transformer, Ns > Np
For step-down transformer, Ns < Np