Projectile motion refers to the motion of an object that is projected into the air at an angle to the horizontal.
Projectile motion relies on the following principles:
- Newton’s first law of motion: an object will continue to move in a straight line with a constant speed (or remain at rest) unless acted on by an unbalanced force.
- Newton’s second law of motion: an object accelerates in the direction of a resultant force acting on it (resultant force = mass × acceleration).
- Projectile paths may be predicted using the equations of motion.
- A vector velocity may be resolved into horizontal and vertical components.
Core assumptions of most projectile motion questions:
- Acceleration due to gravity, g, is constant ($10 \text{ m s}^{-2}$ or $9.81 \text{ m s}^{-2}$) over entire motion and is always directed downwards.
- No horizontal acceleration
- Effect of air resistance is negligible
Path of a projectile without air resistance
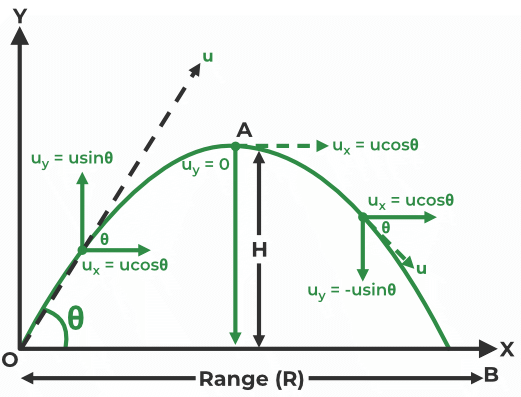
Characteristic of the path of a projectile without air resistance:
- The trajectory is always a parabola
- The diagram is symmetrical about point $A$
- $/theta$ is the angle of projection
- $O$ is the point of projection
- $B$ is the point of impact
- The length $OB$ is the range ($R$) or sometimes treated as displacement $s$ during problem solving
- The time for object to move from point $O$ to the highest point $A$ is equal to the time for the object to move from the highest point $A$ to $B$
| Horizontal Direction | Vertical Direction |
|---|---|
| $u_{x} = u \cos \theta$ | $u_{y} = u \sin \theta$ |
| At highest point $A$, $v_{x} = u_{x}$ | At highest point $A$, $v_{y} = 0$ |
| $a_{x} = 0$ | $a_{y} = -9.81 \text{ m s}^{-2}$ |
| Horizontal displacement = $s_{x}$ | Vertical displacement = 0 |
Horizontal Projectile
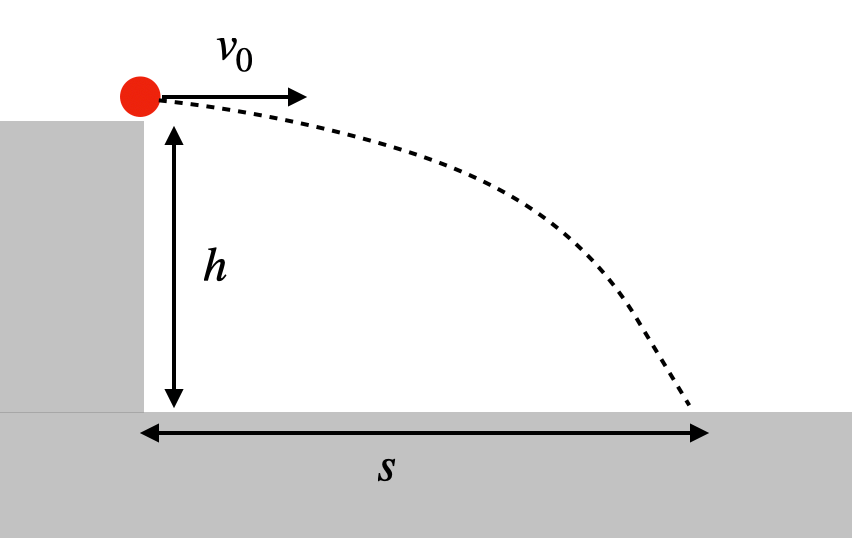
| Horizontal Direction | Vertical Direction |
|---|---|
| $u_{x} = u$ | $u_{y} = 0$ |
| $a_{x} = 0$ | $a_{y} = -9.81 \text{ m s}^{-2}$ |
| Horizontal displacement = $s_{x}$ | Vertical displacement = $-s_{y}$ |
Horizontal projectile at upwards angle
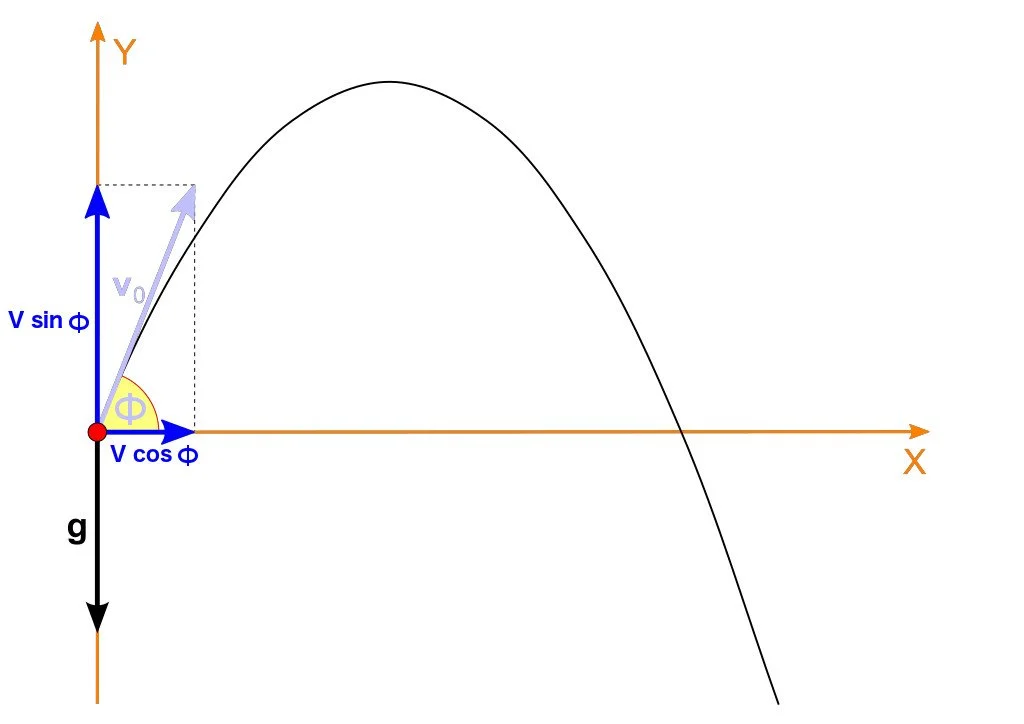
| Horizontal Direction | Vertical Direction |
|---|---|
| $u_{x} = u \cos \theta$ | $u_{y} = u \sin \theta$ |
| At highest point $A$, $v_{x} = u_{x}$ | At highest point $A$, $v_{y} = 0$ |
| $a_{x} = 0$ | $a_{y} = -9.81 \text{ m s}^{-2}$ |
| Horizontal displacement = $s_{x}$ | Vertical displacement = $-s_{y}$ |
Projectile motion at downwards angle
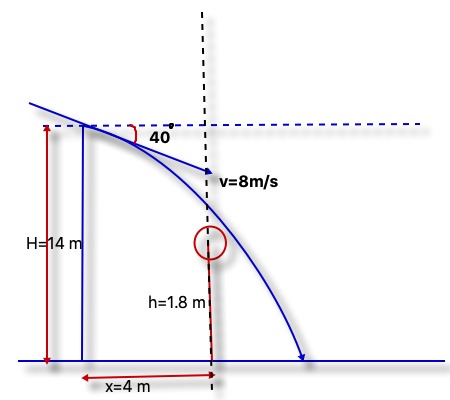
| Horizontal Direction | Vertical Direction |
|---|---|
| $u_{x} = u \cos \theta$ | $u_{y} = u \sin \theta$ |
| $a_{x} = 0$ | $a_{y} = -9.81 \text{ m s}^{-2}$ |
| Horizontal displacement = $s_{x}$ | Vertical displacement = $-s_{y}$ |
Projectile motion with air resistance
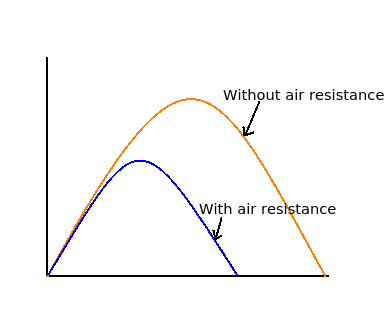
Key Characteristics of Graph:
- Horizontal range of object is shorter
- Maximum height reached is smaller
- Path is asymmetrical about highest point
Horizontally,
- Horizontal velocity no longer constant
- Horizontal velocity decreases with time. Object slows down
- Smaller horizontal range
Vertically,
- Going up, $a_{\text{upwards}} \, = \, g + \frac{F_{\text{Drag} \, \text{Force}}}{m}$
- Going down, $a_{\text{downwards}} \, = \, g-\frac{F_{\text{Drag} \, \text{Force}}}{m}$
Since $\mid a_{\text{upwards}} \mid \, > \, \mid a_{\text{downwards}} \mid$, $\Delta V_{\text{upwards}} \, > \, \Delta V_{\text{downwards}}$. So, object slows down at a faster rate on the way up, time taken to reach maximum point is less than the time taken to reach the ground from the maximum point.
Simulations of projectile motion: http://phet.colorado.edu/en/simulation/projectile-motion
Steps to solve projectile motion questions
Remember to adapt these steps based on the specific details given in each problem, and always be mindful of units and sign conventions.
1. Make a Clearly Labelled Sketch:
- Draw a clear diagram of the projectile motion, including the initial and final positions, as well as the trajectory.
- Label the relevant quantities such as initial velocity $u$, final velocity $v$, acceleration due to gravity $g$, angle of projection $\theta$, and any other given values.
2. Resolve Initial Velocity:
- If given the initial velocity $u$ at an angle $\theta$, resolve it into its horizontal $u_x$ and vertical $u_y$ components.
- $u_x = u \cos(\theta)$
- $u_y = u \sin(\theta)$
3. Analyze Horizontal and Vertical Motion Separately:
- Break down the motion into horizontal and vertical components.
- For horizontal motion, there is no acceleration, so the velocity remains constant $u_x$.
- For vertical motion, use the acceleration due to gravity $g = 9.81 \, \text{m/s}^2$ and the initial vertical velocity $u_y$.
4. Sign Convention:
- Decide on a sign convention for motion. It’s common to take upward as positive and downward as negative. Be consistent with this convention throughout the problem.
5. Apply Kinematics Equations:
- For horizontal motion $x$:
- $x = u_x \times t$ (where $t$ is the time of flight)
- For vertical motion $y$:
- $y = u_y t + \frac{1}{2} g \times t^2$ (use this when calculating vertical displacement), where $g$ is negative
- $v_y = u_y + g \times t$ (use this to find the final vertical velocity), where $g$ is negative
6. Use Special Points in Motion:
- At the highest point of the trajectory, vertical velocity $v_y$ is zero.
- At the end of the motion, when the projectile hits the ground, $y = 0$.
7. Check for Symmetry:
- If the projectile lands at the same vertical level as it was launched, the time of ascent equals the time of descent.
8. Solve for Unknowns:
- Plug in the known values into the equations and solve for the unknowns.
- Always pay attention to the units and make sure they are consistent.
9. Verify Results:
- Ensure that your results make physical sense. Check if the signs and magnitudes align with the expected behavior of the projectile.
10. Practice:
- The more you practice, the more comfortable you will become with applying these steps and solving projectile motion problems.
Worked Examples
Example 1
A rescue plane is flying horizontally with a speed of 50 m s-1 and at an altitude of 200 m above the sea when it drops a warning flare.
Neglecting air resistance and assuming that the plane does not change its course, speed or altitude, how far from the plane is the flare when it hits the water?
Click here to show/hide answer
The flare will be released with the same horizontal velocity of 50 m s-1. Since there is no acceleration in the horizontal direction, the flare will be directly below the position of the plane when it hits the water
Answer: 200 m
Example 2
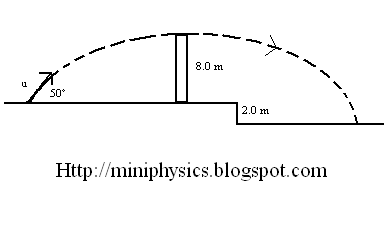
A ball was kicked over a 8.0m wall as shown below with a velocity u at an angle of 50° above the horizontal. At the highest point of the trajectory, the ball managed to just go over the wall. It landed into a depression 2.0 m deep.
a) Express the initial horizontal velocity and initial vertical velocity in terms of u.
b) Calculate the initial speed of the ball
c) Calculate the vertical velocity of the ball vy just before it hits the depression.
d) Hence, or otherwise, calculate the velocity of the ball v just before it hits the depression, and the angle it makes below the horizontal.
e) Calculate the time of flight
Click here to show/hide answer
a)
$$u_x = u \cos 50°$$
$$u_y = u \sin 50°$$
b) Taking upwards and rightwards as positive, consider the ball at its highest point of its trajectory:
$$ \begin{aligned} v_y^2 &= u_y^2 + 2a_y s_y \\ 0 &= (u \sin 50°)^2 + 2(-9.81)(8.0) \\ u &= 16.355 \\ u &= 16 \, \text{m s}^{-1} \end{aligned}$$
c)
$$ \begin{aligned} v_y^2 &= u_y^2 + 2a_y s_y \\ v_y^2 &= (16.355 \sin 50°)^2 + 2(-9.81)(-2.0) \\ v_y^2 &= 196.2 \\ v_y &= -14.007 \\ v_y &= -14 \, \text{m s}^{-1} \end{aligned}$$
d)
$$ \begin{aligned} v^2 &= v_x^2 + v_y^2 \\ v^2 &= (16.355 \cos 50°) + (-14.007)^2 \\ v &= 17.513 \\ v &= 17 \, \text{m s}^{-1} \end{aligned}$$
$$ \begin{aligned} \tan \theta &= \frac{v_y}{v_x} \\ \tan \theta &= \frac{14.007}{16.355 \cos 50°} \\ \theta &= 53.111° \\ \theta &= 53° \end{aligned}$$
The velocity of the ball is $17 \, \text{m s}^{-1}$ at an angle of $53°$ below the horizontal.
e)
$$\begin{aligned} v_y &= u_y + a_y t \\ -14.007 &= (16.335 \sin 50°) + (-9.81)t \\ t &= 2.7049 \\ t &= 2.7 \, \text{s} \end{aligned}$$
Example 3
A ball is projected horizontally from the top of a building. One second later, another ball is projected horizontally from the same point with the same velocity. At what point in the motion will the balls be closest to each other? Will the first ball always be travelling faster than the second ball? What will be the time interval between the moments when the two balls hit the ground? Can the horizontal projection velocity of the second ball be changed so that the balls arrive at the ground at the same time?
Click here to show/hide answer
The balls will be closest together as the second ball is thrown. Yes, the first ball will always be moving faster, since its flight time is larger, and thus the vertical component of the velocity is larger. The time interval will be one second. No, since the vertical component of the motion determines the flight time.
Example 4
The maximum range of a projectile occurs when it is launched at an angle of 45° with the horizontal, if air resistance is ignored. If air resistance is not ignored, will the optimum angle be greater or less than 45.0°? Explain.
Click here to show/hide answer
The optimal angle would be less than 45°. The longer the projectile is in the air, the more that air resistance will change the components of the velocity. Since the vertical component of the motion determines the flight time, an angle less than 45° would increase range.
Example 5
A sailor drops a wrench from the top of a sailboat’s mast while the boat is moving rapidly and steadily in a straight line. Where will the wrench hit the deck?
Click here to show/hide answer
The wrench will hit at the base of the mast. If air resistance is a factor, it will hit slightly leeward of the base of the mast, displaced in the direction in which air is moving relative to the deck. If the boat is scudding before the wind, for example, the wrench’s impact point can be in front of the mast.