Table of Contents
Refraction Of Light
Refraction of light is the change in direction (bending of light rays) when it passes from one optically transparent medium to another.
- When light passes from one medium to another (for example, from air into glass), it changes direction. This change in direction is called refraction. The refractive index (covered below) helps us understand how much the light will bend when it enters a new medium.
Key Terms Used In Refraction Of Light
Refracted ray is the bent ray as a result of passing from one optical medium to another.
Normal is an imaginary line perpendicular to the interface of media where the refraction occur.
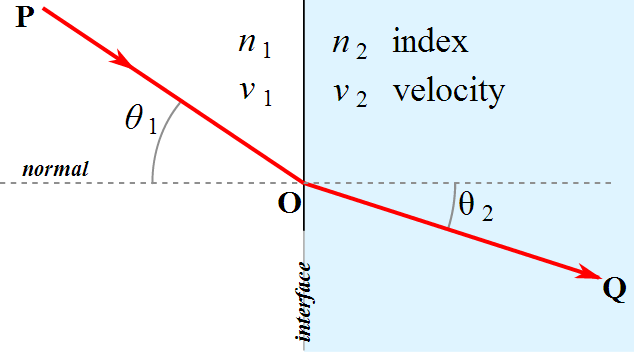
Angle of incidence, $i$, is the angle between incident ray and the normal.
Angle of refraction, $r$, is the angle between refracted ray and the normal.
Laws of Refraction
First law of refraction states that the incident ray, the refracted ray and the normal to the interface all lie in the same plane.
Second law of refraction states that for two given media, the ratio $\frac{\sin \, i}{\sin \, r} = \text{ constant}$, where $i$ is the angle of incidence and $r$ is the angle of refraction.
Refractive Index
The refractive index is a measure of how much the speed of light is reduced inside a medium compared to the speed of light in a vacuum.
The refractive index ($n$) of a material is defined as the ratio of the speed of light in a vacuum ($c$) to the speed of light in the material ($v$). It is given by the formula:
$$n = \frac{c}{v}$$
The refractive index is also given by the formula:
$$n = \frac{\sin \, i}{\sin \, r}$$
Key Points Of Refractive Index
- The refractive index of a medium is always greater than 1, since light travels slower in any medium than it does in a vacuum. For example, the refractive index of air is approximately 1.0003, and for typical glass, it’s around 1.5. This means light travels about 1.5 times slower in glass than in a vacuum.
- The greater the value of the refractive index of a medium, the greater is the “bending” effect (refraction) of light when it passes from air into that medium.
- A material with a larger value of n is an optically denser medium.
- The higher the refractive index of a medium, the slower will be the speed of light through it. This means that a medium’s optical density increases as its refractive index increases.
Snell’s Law
Snell’s Law relates the angle of incidence (the angle the incoming light ray makes with the normal to the surface) to the angle of refraction (the angle the refracted ray makes with the normal). Snell’s Law is given by:
$$n_1 \sin(\theta_i) = n_2 \sin(\theta_r)$$
where $n_1$ and $n_2$ are the refractive indices of the first and second mediums, and $\theta_i$ and $\theta_r$ are the angles of incidence and refraction, respectively.
Behaviour Of Refraction Of Light
Light travelling from:
- denser medium to less dense medium – Bend away from normal
- less dense medium to denser medium – Bend towards normal
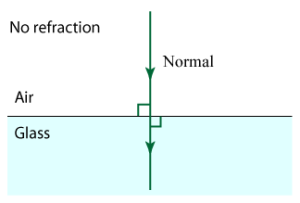
However, if the light ray enters another medium perpendicularly to the boundary, there is no deviation of the ray even when there is change in speed of light.
Consequence Of Refraction Of Light: Apparent Depth
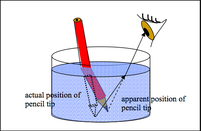
Apparent depth is a concept in physics that illustrates the optical illusion created by the refraction of light when it passes from one medium to another with a different refractive index. When you look at an object submerged in a transparent medium like water, glass, or clear plastic, it appears to be at a shallower depth than it actually is. This phenomenon is known as apparent depth.
The cause of this illusion is the refraction of light. Refraction occurs when light waves travel from one medium to another at an angle and change speed due to the difference in the optical density of the two media. This change in speed causes the light rays to bend.
When light rays travel from a denser medium (like water) into a less dense medium (like air), they bend away from the normal line (an imaginary line perpendicular to the surface at the point of incidence). As a result, when you observe the object, your brain traces the light rays back along a straight line into the water. Because the rays have bent, the object appears to be higher, or closer to the surface, than it really is.
The relationship between the actual depth $d$, apparent depth $d’$, and the refractive index of the medium $n$ can be understood through a simple formula:
$$n = \frac{d}{d’}$$
This equation highlights that the apparent depth $d’$ is smaller than the actual depth $d$ for a medium with a refractive index greater than 1 (which is the case for most transparent materials).
Examples Of Apparent Depth
A common example of apparent depth is when a swimming pool appears shallower than it truly is. Another is the apparent bending of a straw placed in a glass of water.
Refractive Index & Wavelengths Of Light
For visible light, the refractive indexes of most transparent medium decrease with increasing wavelength. Hence,
$$1 < n \left( \lambda_{\text{red}} \right) < n \left( \lambda_{\text{green}} \right) < n \left( \lambda_{\text{blue}} \right)$$
This causes white light to split in its constituent colours (rainbow) when it passes through a prism.
Additional notes about speed of light in medium (v): (OPTIONAL)
Light is not actually “slowed” by the medium. The speed of light is ALWAYS c. This constancy of the speed of light plays a major role in the theory of special relativity by Einstein. (In fact it is built into modern Physics theories) The speed of light in medium used in the calculation above is actually the apparent speed of light in that medium. When light passes through a medium, it is constantly being absorbed and re-emitted by the electrons in the air molecules. However, the re-emission of light is not instantaneous as the electrons “play” with the light for a short while before re-emitting it. This causes the apparent slower speed of light.
Note: The absorption and re-emission of light actually contributes to the development of lasers. You will be able to learn more about this if you choose to study Physics in A level.
Dispersion Of Light By A Prism
When light passes through a prism, a remarkable phenomenon occurs: the light is dispersed into its constituent colors, a process known as dispersion. This phenomenon is not only fascinating to observe but also serves as a practical demonstration of the laws of refraction and the concept of refractive index, providing insights into the fundamental properties of light.
The Process Of Dispersion
Dispersion occurs because different colors (or wavelengths) of light bend by different amounts when they pass from one medium into another. In the context of a prism, which is typically made of glass, light enters the glass and slows down, because the speed of light in glass is less than its speed in air. This slowing down causes the light to bend at an angle—a process known as refraction (as discussed above). However, not all colors slow down by the same amount: shorter wavelengths (blue and violet light) slow down more and are refracted more than longer wavelengths (red light).
Link To Laws Of Refraction
This differential bending of light by wavelength is directly linked to Snell’s law of refraction, which states that the ratio of the sine of the angle of incidence to the sine of the angle of refraction is a constant, known as the refractive index. The formula is given as $n_1 \sin(\theta_1) = n_2 \sin(\theta_2)$, where $n_1$ and $n_2$ are the refractive indices of the air and the glass, respectively, and $\theta_1$ and $\theta_2$ are the angles of incidence and refraction. Because the refractive index varies slightly with the wavelength of light, different colors are refracted by different amounts, leading to the dispersion of white light into a spectrum of colors.
Refractive Index & Dispersion
The refractive index’s dependence on wavelength (chromatic dispersion) is a key reason why a prism can separate white light into its constituent colors. Materials with a higher refractive index will generally disperse light more than those with a lower refractive index. This principle is not only fundamental in understanding how prisms work but also has practical applications in lenses, binoculars, and various optical instruments to correct for chromatic aberration—a distortion in which there is a failure to focus all colors to the same convergence point.
Worked Examples
Example 1
The refractive index of an optically clear material is 1.6. What is the angle of refraction if the angle of incidence is $22^{\circ}$.
Click here to show/hide answer
$$\begin{aligned} n &= \frac{\sin i}{\sin r} \\ \sin r &= \frac{\sin i}{n} \\ \sin r &= \frac{\sin 22^{\circ}}{1.6} \\ r &= 13.5^{\circ} \end{aligned}$$
Example 2
Find the angle at which light bends when passing through a specific type of glass with a refractive index of 1.55, given an incident angle of $25^{\circ}$.
Click here to show/hide answer
$$\begin{aligned} n &= \frac{\sin i}{\sin r} \\ \sin r &= \frac{\sin i}{n} \\ \sin r &= \frac{\sin 25^{\circ}}{1.55} \\ r &= 15.8^{\circ} \end{aligned}$$
Example 3: Basic Refraction Concept
Explain why a pencil appears bent when partially submerged in water, using the concept of refraction.
Click here to show/hide answer
The pencil appears bent due to the refraction of light. When light rays travel from water (denser medium) to air (less dense medium), they bend away from the normal line due to the change in speed of light in different media. This bending causes the part of the pencil submerged in water to appear at a different position to the observer above water, making the pencil look bent.
Example 4: Refractive Index Calculation
The speed of light in a vacuum is approximately $3 \times 10^8$ m/s. If light travels through a diamond at a speed of $1.24 \times 10^8$ m/s, what is the refractive index of diamond?
Click here to show/hide answer
The refractive index $n$ of diamond can be calculated using the formula $n = \frac{c}{v}$, where $c$ is the speed of light in a vacuum and $v$ is the speed of light in the medium (diamond). Plugging in the given values: $n = \frac{3 \times 10^8}{1.24 \times 10^8} = 2.42$. Therefore, the refractive index of diamond is 2.42.
Example 5: Applying Snell’s Law
A light ray enters glass $n = 1.5$ from air $n = 1$ with an angle of incidence of 30°. Use Snell’s Law to find the angle of refraction within the glass.
Click here to show/hide answer
Snell’s Law is given by $n_1 \sin(\theta_1) = n_2 \sin(\theta_2)$. Substituting the given values: $1 \times \sin(30°) = 1.5 \times \sin(\theta_2)$. Solving for $\theta_2$, we find that $\sin(\theta_2) = \frac{\sin(30°)}{ 1.5}$. Calculating this gives $\theta_2 \approx 19.47°$.
Example 6: Understanding Apparent Depth
A fish is swimming 1 meter below the surface of a lake. If the refractive index of water is 1.33, how deep does the fish appear to be to an observer outside the lake?
Click here to show/hide answer
The formula for apparent depth $d’$ is $d’ = \frac{d}{n}$, where $d$ is the actual depth, and $n$ is the refractive index. Substituting the given values: $d’ = \frac{1}{1.33} \approx 0.75$ meters. Therefore, the fish appears to be approximately 0.75 meters deep.
Example 7: Refractive Index & Optical Density
Explain why a material with a higher refractive index is considered optically denser and how this affects the speed of light through the material.
Click here to show/hide answer
A higher refractive index indicates that light travels slower in the material compared to a vacuum, implying the material is optically denser. This is because the refractive index is directly related to how much the speed of light is reduced inside the medium. Thus, the higher the refractive index, the slower the light speed, indicating a greater optical density. This affects light’s behavior, including its bending (refraction) when transitioning between media of different optical densities.
Example 8: Wavelengths & Refractive Index
Describe how the refractive index of transparent mediums changes with the wavelength of light and the consequence of this on the dispersion of white light through a prism.
Click here to show/hide answer
The refractive index of most transparent mediums decreases with increasing wavelength of light. This means that shorter wavelengths (blue light) are bent more than longer wavelengths (red light) when passing through a medium like a prism. As a result, white light, which is a mixture of different wavelengths, is split into its constituent colors, creating a spectrum or rainbow. This phenomenon, known as dispersion, occurs because each color is refracted at a slightly different angle due to the variation in refractive index with wavelength.
Example 9: Calculating Refractive Index (Prism)
A beam of white light enters a glass prism with an angle of incidence of 30 degrees. The angle of refraction inside the prism for the red component of the light is observed to be 22 degrees. Knowing that the refractive index of air is approximately 1, calculate the refractive index of the glass for the red component of the light.
Click here to show/hide answer
To find the refractive index of the glass for the red component, we use Snell’s law, $n_1 \sin(\theta_1) = n_2 \sin(\theta_2)$.
Given:
- $n_1 = 1$ (refractive index of air),
- $\theta_1 = 30^\circ$ (angle of incidence),
- $\theta_2 = 22^\circ$ (angle of refraction for red light).
We need to find $n_2$ (refractive index of glass for red light).
Rearranging Snell’s law gives us:
$$n_2 = \frac{n_1 \sin(\theta_1)}{\sin(\theta_2)}$$
Substituting the given values:
$$n_2 = \frac{1 \times \sin(30^\circ)}{\sin(22^\circ)}$$
Using a calculator:
$$n_2 \approx \frac{0.5}{0.3746} \approx 1.334$$
Therefore, the refractive index of the glass for the red component of the light is approximately 1.334.
Example 10: Speed of Light in Prism
The refractive index of a glass prism for violet light is 1.54, and for red light, it is 1.51. Given the speed of light in vacuum is approximately $3.00 \times 10^8$ m/s, calculate the speed of violet and red light within the prism.
Click here to show/hide answer
The speed of light in a medium is given by $v = \frac{c}{n}$, where $c$ is the speed of light in vacuum, and $n$ is the refractive index of the medium.
- For Violet Light:
- $n_{\text{violet}} = 1.54$,
$$v_{\text{violet}} = \frac{3.00 \times 10^8 \text{ m/s}}{1.54} \approx 1.948 \times 10^8 \text{ m/s}$$
- For Red Light:
- $n_{\text{red}} = 1.51$,
$$v_{\text{red}} = \frac{3.00 \times 10^8 \text{ m/s}}{1.51} \approx 1.987 \times 10^8 \text{ m/s}$$
Therefore, the speed of violet light within the prism is approximately $1.948 \times 10^8$ m/s, and the speed of red light within the prism is approximately $1.987 \times 10^8$ m/s, demonstrating how the refractive index affects the speed of different colors of light within a medium.
[OPTIONAL] Example 11: Angle of Dispersion
A prism has an angle of prism of 60 degrees. When a beam of white light passes through the prism, the angle of deviation for the violet light is measured to be 40 degrees, whereas for the red light it is 35 degrees. Calculate the angle of dispersion produced by the prism.
Click here to show/hide answer
The angle of dispersion is the difference between the angles of deviation for the violet and red light.
Given:
- Angle of deviation for violet light = 40 degrees,
- Angle of deviation for red light = 35 degrees.
$$\text{Angle of dispersion} = 40^\circ-35^\circ = 5^\circ$$
Therefore, the prism produces an angle of dispersion of 5 degrees.