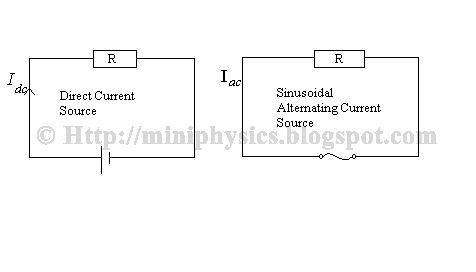
The root-mean-square (r.m.s.) value of an alternating current is equivalent to the steady direct current that converts electrical energy to other forms of energy at the same average rate as the alternating current in a given resistance.
- The r.m.s. current of an alternating current is also known as the effective current of the a.c.
- An alternating current ammeter reads the root-mean-square current value of an alternating current.
- The r.m.s. value of an alternating current is the equivalent direct current which could have achieved the same amount of heating over the same period of time for the same resistor used.
For the left diagram,
The power dissipated in R is $P_{dc} = I_{dc}^{2} \, R$
For right diagram,
Average power is $\left< P_{ac} \right> \, = \, \left< I_{ac}^{2} \right> \, R$
Supposing both resistors are dissipating heat at the same average rate:
$P_{dc} = \left< P_{ac} \right>$
$I_{dc}^{2} \, R = \left< I_{ac}^{2} \right> R$
Canceling R from both sides of the equation,
$I_{dc}^{2} \, = \left< I_{ac}^{2} \right>$
$I_{dc} = \sqrt{ \left( \left< I_{ac}^{2} \right>\right) }= I_{rms}$
The steady $I_{dc}$ is equivalent to the square root of the mean of the square of the $I_{ac}$
3 simple steps to get r.m.s. values
- Square the current
- Take the mean or average
- Square root the mean
For a sinusoidal alternating current, where Io is the peak value
$$I_{rms} = \frac{I_{o}}{\sqrt{2}}$$
$$V_{rms} = \frac{V_{o}}{\sqrt{2}}$$