Table of Contents
Equilibrium
A rigid body is considered to be in equilibrium, if there is:
- Translational equilibrium; AND
- Rotational Equilibrium.
A body in equilibrium experiences NO acceleration and will remain in equilibrium indefinitely, UNLESS it is disturbed by an external force. (Newton’s First Law)
Translational Equilibrium
Translational equilibrium is obtained when the resultant force or vector sum of all forces acting upon the rigid body is zero. In simpler terms, this means that:
- forces pointing to left = forces pointing to right; AND
- forces pointing up = forces pointing down
- Linear acceleration of object is zero
Rotational Equilibrium (Principle Of Moments)
Rotational equilibrium is obtained when the algebraic sum of the torques is zero.
However, it can also be interpreted as:
The principle of moments states that for a body to be in rotational equilibrium, the sum of clockwise torques about any point (which acts as a pivot) must equal to the sum of anti-clockwise torques about the same point.
Sum of clockwise torques = sum of anti-clockwise torques
Recap: Torque = moment of force
- Angular acceleration of object is zero
- Lines of action of all forces acting on the object intersect at a point
Summary
In summary, the conditions for object to be in equilibrium:
- The sum of moments about any point is zero – resultant moment on the object is zero. (Rotational equilibrium – Principle of moments)
- The vector sum of forces on object is zero – resultant force on the object is zero. (Translational equilibrium)
Steps To Solve Equilibrium Problems
Solving equilibrium problems involves a systematic approach. Here are the steps:
Steps To Solve Equilibrium Problems
1. Isolate Body of Interest:
- Identify the specific object or system you are analyzing.
2. Identify Forces:
- Consider all forces acting directly on the isolated body.
- Include gravitational forces, applied forces, tension, normal forces, friction, etc.
3. Draw Free Body Diagram (FBD):
- Sketch a clear and accurate diagram representing the isolated body.
- Use arrows to denote forces with the correct magnitude and direction.
- Clearly label each force.
4. Coordinate System:
- Establish a coordinate system for analysis. This is often chosen based on the geometry or symmetry of the problem.
5. Apply Equilibrium Conditions:
- For translational equilibrium, sum all forces in both x and y directions and set them equal to zero.
- For rotational equilibrium, sum all torques (moments) and set them equal to zero.
- Write out the equations based on your coordinate system.
Steps To Solve Rotational Equilibrium Problems
1. Follow Steps 1-4 from the Equilibrium Problems:
2. Calculate Torque:
- Identify the axis of rotation.
- Calculate the torque for each force by multiplying its magnitude by the perpendicular distance from the axis.
3. Apply Rotational Equilibrium Condition:
- Sum all torques and set them equal to zero.
- This equation ensures that the object is not rotating.
Steps To Solve Translational Equilibrium Problems:
1. Follow Steps 1-4 from the Equilibrium Problems:
2. Resolve Forces:
- If forces are not purely along the x or y-axis, resolve them into their respective components.
- Ensure that the resolved forces align with your chosen coordinate system.
3. Apply Translational Equilibrium Condition:
- Sum all forces in the x and y directions and set them equal to zero.
- This equation ensures that the object is not accelerating in any direction.
Additional Tips On Solving Equilibrium Problems
- Include Direction:
- Pay attention to the direction of the forces. Include signs in your equations to denote direction.
- Check Units:
- Ensure that all forces and distances are in consistent units.
- Use Algebra:
- Solve the equations algebraically for unknowns.
Worked Examples
Example 1
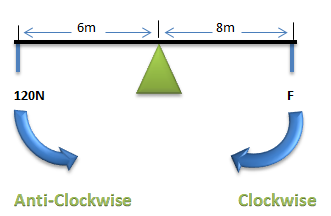
Consider the diagram above, whereby a plank is supported by a pivot. Two forces, 120 N and F are acting on the plank. Given that the plank is perfectly balanced (has rotational equilibrium), find F.
Click here to show/hide answer
Recall that moment of force is calculated by:
$$r = F \times d$$
Anti-clockwise moment:
$$\begin{aligned} r_{\text{anti-clockwise}} &= F \times d \\ &= 120 \times 6 \\ &= 720 \text{ Nm} \end{aligned}$$
Clockwise moment:
$$\begin{aligned} r_{\text{clockwise}} &= F \times d \\ &= F \times 8 \\ &= 8F \end{aligned}$$
Since there is rotational equilibrium, we know that $r_{\text{anti-clockwise}} = r_{\text{clockwise}}$ from the principle of moments.
$$\begin{aligned} r_{\text{clockwise}} &= 8F \ r_{\text{anti-clockwise}} &= 8F \\ 720 &= 8F \\ F &= 90 \text{ N}\end{aligned}$$
Example 2
State the Principle of Moments and discuss how this principle may be applied to two persons of different weights trying to balance on a see-saw.
Click here to show/hide answer
The principle of moments states that for a body to be in rotational equilibrium, the sum of clockwise torques about any point (which acts as a pivot) must equal to the sum of anti-clockwise torques about the same point.
For the see-saw to be balanced, the see-saw must be in rotational equilibrium – which mandates that the clockwise moment about the pivot be equal to the anti-clockwise moment about the same pivot.
Since the two persons have different weights, varying the perpendicular distances to the pivot is the only way for the clockwise and anti-clockwise moment to be equal.
Consider that the two persons are labelled as 1 and 2, with:
- their weights labelled as $W_{1}$ and $W_{2}$, whereby $W_{1} > W_{2}$.
- their distance away from the pivot of the see-saw labelled as $d_{1}$ and $d_{2}$
Recall that moment of force is calculated by:
$$r = F \times d$$
For the see-saw to be balanced:
$$\begin{aligned} r_{\text{clockwise}} &= r_{\text{anti-clockwise}} \\ W_{1} \times d_{1} &= W_{2} \times d_{2} \end{aligned}$$
Since $W_{1} > W_{2}$, $d_{1}$ must be smaller than $d_{2}$ for the see-saw to be balanced. (I.e. The heavier person will have to sit closer to the pivot.)
Example 3
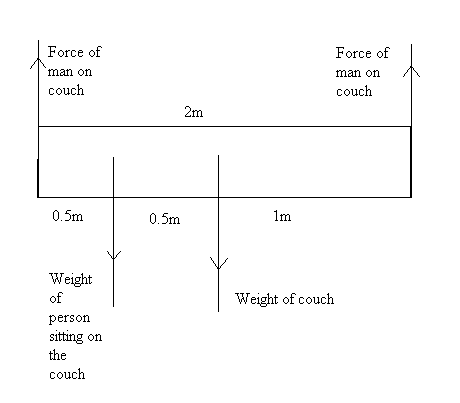
Two people are carrying a 2 m long couch with a mass of M = 20 kg level with the horizontal by lifting it from it ends. The center of mass of the couch is 1 m from each end. While it is being carried, another person with a mass m of 60 kg sits on the couch 0.5 m from one end. How much force will each person carrying the couch have to exert upwards in order to continue carrying the couch levelly?
Click here to show/hide answer
The couch above is in equilibrium : Rotational equilibrium and translational equilibrium.
Taking moments about the left point,
$$\begin{aligned} \text{Anti-clockwise moments about left point} &= \text{Clockwise moments about right point} \\ F_{\text{By right person}} \times 2 &= F_{\text{Weight of person on couch}} \times 0.5 + F_{\text{Weight of couch}} \times 1 \\ F_{\text{By right person}} \times 2 &= (60)(9.8)(0.5) + (20)(9.8)(1) \\ F_{\text{By right person}} &= \frac{490}{2} \\ F_{\text{By right person}} &= 245 \, \text{N} \end{aligned} $$
Taking moments about the right point,
$$ \begin{aligned} \text{Clockwise moments about right point} &= \text{Anti-clockwise moments about left point} \\ F_{\text{By left person}} \times 2 &= F_{\text{Weight of person on couch}} \times 1.5 + F_{\text{Weight of couch}} \times 1 \\ F_{\text{By left person}} \times 2 &= (60)(9.8)(1.5) + (20)(9.8)(1) \\ F_{\text{By left person}} &= 539 \, \text{N} \end{aligned}$$
Answer: 245N and 539N