Series & Parallel Circuits

Series Circuits

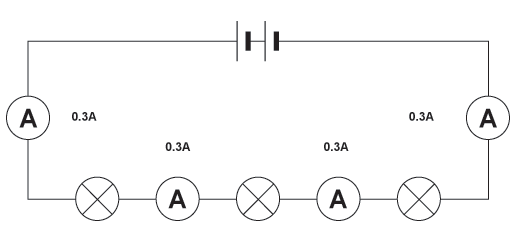
In series circuits, each component is connected in a sequence on the same path. Series circuits has the same current through each circuit components BUT different potential difference across each circuit components.

Same Current Flow

Single Path for Charge: In a series circuit, electrical charge travels along a singular path, sequentially passing through each connected component. This unified path ensures a consistent flow of charge across all components.
Consistent Current: Due to the unidirectional flow of charge, the current is identical at all points in a series circuit, regardless of the number or type of components.
Impact of Additional Components: Introducing a new component into a series circuit invariably affects the overall current flow. Since each component adds resistance, the total current throughout the circuit diminishes accordingly.

Different Potential Difference

Definition of Potential Difference: The potential difference (or voltage) between two points in a circuit correlates with the energy expended to move charge through components situated between those points. Total energy dissipation can be calculated by summing individual dissipations.
Voltage Distribution: In series circuits, the sum of potential differences across all components (e.g., bulbs) equates to the total electromotive force (EMF) supplied by the sources (e.g., battery).
Component Resistance and Voltage: The component with the highest resistance within a series circuit typically exhibits the greatest potential difference, excluding the battery’s contribution.
Negligible Wire Voltage Drop: The potential difference across connecting wires is virtually zero due to minimal energy loss, ensuring efficient energy transfer within the circuit.

Parallel Circuits

Parallel circuits has the different current through each branch (same current through the circuit components within the branch) BUT same potential difference across each branch. (different potential difference across the circuit components within the branch)

Different Currents

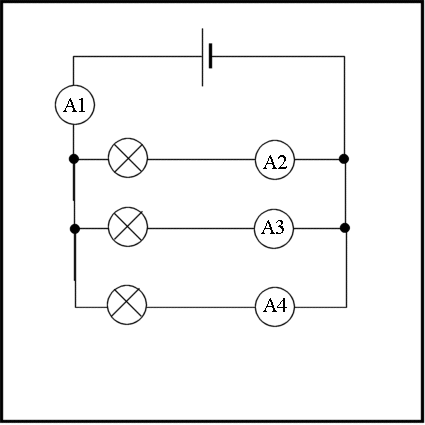
Multiple Paths for Charge: Contrary to series configurations, parallel circuits provide several paths for charge flow. This multiplicity does not alter the total charge emanating from the source.
Summation of Branch Currents: The overall current supplied by the source is the cumulative sum of currents flowing through each branch.
Resilience to Component Changes: Removal or addition of a lamp in a parallel circuit does not affect the functionality of others, showcasing the independence of parallel pathways. This characteristic underpins the design of most household lighting systems.
Current and Resistance Relationship: The branch with the lowest resistance attracts the highest current, demonstrating the inverse relationship between current flow and resistance.
Charge Conservation at Junctions: The principle of charge conservation mandates that the total current entering any junction must equal the total current exiting, ensuring continuity of flow.

Same Potential Difference

Equal Voltage Across Components: In parallel circuits, components connected across the same two points share an identical potential difference. This uniformity ensures that each component operates under the same voltage conditions, regardless of the current flowing through individual branches.
Consistent Branch Voltage: The potential difference across each branch of a parallel circuit matches that of the source, allowing for equal energy distribution among components.

Advantages & Disadvantages Of Using Series Vs Parallel Circuits

Circuit Type	Advantages	Disadvantages
Series Circuits	Simpler design and easier to construct. Less expensive as it requires fewer components. Current is the same through all components, making it easy to calculate.	If one component fails, the entire circuit stops working. Adding more components increases total resistance, reducing overall current. Not suitable for circuits that require components to operate independently.
Parallel Circuits	More reliable; if one component fails, the rest of the circuit remains functional. Each component operates independently, with the same voltage across each. Suitable for complex electrical systems, like those in buildings and vehicles.	More complex design and harder to construct. Requires more wiring, making it more expensive. Calculating total resistance can be more complicated due to different current paths.

Calculations and Formulas

Understanding how to calculate total resistance, current, and voltage in series and parallel circuits is fundamental in electronics. These calculations are based on Ohm’s Law, which states that the current through a conductor between two points is directly proportional to the voltage across the two points and inversely proportional to the resistance between them. The formula is given by $V = IR$, where $V$ is the voltage across the resistor, $I$ is the current flowing through the resistor, and $R$ is the resistance.

Series Circuits

In a series circuit:

Total Resistance ($R_{\text{total}}$): The total resistance is the sum of all individual resistances. If you have resistors $R_1, R_2, …, R_n$ connected in series, the total resistance is $R_{\text{total}} = R_1 + R_2 + … + R_n$.
Current ($I$): The current is the same through each component in the circuit. Using Ohm’s Law, $I = \frac{V_{\text{total}}}{R_{\text{total}}}$, where $V_{total}$ is the total voltage supplied by the source.
Voltage across each resistor ($V_i$): The voltage across each resistor can be found by $V_i = I \times R_i$, where $I$ is the current through the circuit and $R_i$ is the resistance of the individual resistor.

Parallel Circuits

In a parallel circuit:

Total Resistance ($R_{total}$): The total resistance in a parallel circuit is found using the reciprocal sum of the individual resistances: $\frac{1}{R_{\text{total}}} = \frac{1}{R_1} + \frac{1}{R_2} + … + \frac{1}{R_n}$.
Current ($I$): The total current is the sum of the currents through each parallel branch. Ohm’s Law applies to each branch individually: $I_{\text{total}} = I_1 + I_2 + … + I_n$, where $I_x = \frac{V}{R_x}$ for each branch $x$.
Voltage ($V$): The voltage across each branch in a parallel circuit is the same and equal to the source voltage, $V_{\text{total}}$.

Hybrid Circuits (Series-Parallel Circuits)

Hybrid circuits combine elements of both series and parallel configurations, offering flexibility and efficiency in managing currents, voltages, and resistances within the same circuit. These circuits are prevalent in complex electronic devices, automotive systems, and household appliances.

Advantages of Hybrid Circuits:

Versatility: They can distribute power efficiently across different components with varying power needs.
Reliability: By combining series and parallel paths, these circuits ensure that a failure in one path does not necessarily compromise the entire system.
Customization: Allows for precise control over voltage and current levels across different parts of the circuit, optimizing performance for specific tasks.

Use Cases:

Electronics: In devices like smartphones and computers, where different components require different voltage levels.
Automotive Systems: In vehicle electrical systems, combining series and parallel circuits helps manage lighting, sensors, and other electronic controls efficiently.
Solar Panels: Arrays often use hybrid configurations to balance efficiency and reliability, ensuring consistent power output under varying conditions.

Worked Examples

Example 1: Series Circuit Resistance and Current

You have three resistors in a series circuit connected to a 12V battery. The resistors have values of 2Ω, 3Ω, and 5Ω. Calculate the total resistance of the circuit and the current flowing through it.