Consider an observer O’ on a train moving at velocity v relative to the ground. A mirror is fixed on the ceiling of the train carriage. An observer O is outside the train and stationary relative to the ground.
A pulse of light directed toward the mirror is emitted, and at some time later after reflecting from the mirror, the pulse arrives back at the laser. Observer O’ measure the time interval $\Delta t_{p}$. Because the light pulse has speed c, the time it takes to travel from point A to the mirror and back to point A is $\Delta t_{p} = \frac{2d}{c}$.
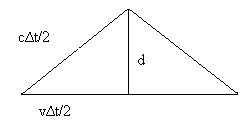
Now consider the same set of events as viewed by O in a second frame. According to this observer, the mirror and laser are moving to the right with a speed v, and as a result the sequence of events appears different. The observer O will see the light leaving the source at an angle with respect to the vertical direction. According to second postulate of special theory of relativity, both observers must measure c for the speed of light.
$$\begin{aligned} \left( \frac{c\Delta t}{2} \right)^{2} &= \left( \frac{v \Delta t}{2} \right)^{2} + d^{2} \\ \Delta t &= \frac{2d}{c\sqrt{1 – \frac{v^{2}}{c^{2}}}} \end{aligned}$$
Because $\Delta t_{p} = \frac{2d}{c}$, we can express the result as:
$$\Delta t = \frac{\Delta t_{p}}{\sqrt{1 – \frac{v^{2}}{c^{2}}}} = \gamma \Delta t_{p}$$
A clock moving past an observer at a speed v runs more slowly than an identical clock at rest with respect to the observer by a factor of $\frac{1}{\gamma}$.
Proper time, $\Delta t_{p}$ is the time interval between two events as measured by an observer who sees two events occur at the same position.
If you are having trouble visualising the above, view the video below.
Video explaining time dilation:
https://www.youtube.com/watch?v=KHjpBjgIMVk