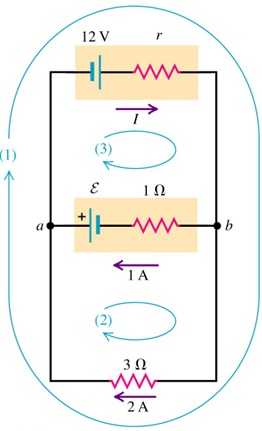
In the circuit shown, a 12 V power supply with unknown internal resistance r is connected to a run-down rechargeable battery with unknown emf $\epsilon$ and internal resistance 1 $\Omega$, and to an indicator light bulb of resistance 3 $\Omega$ carrying a current of 2 A. The current through the run down battery is 1 A in the direction shown. Find the unknown current I, the internal r, and the emf $\epsilon$.
Find the power delivered by the 12 V power supply and by the battery being recharged, and find the power dissipated in each resistor.
Loop 1:
$$\begin{aligned} 12 &= Ir + 6 \\ Ir &= 6 \, \text{V} \end{aligned}$$
Loop 2:
$$\begin{aligned} – \epsilon &= -1 + 6 \\ \epsilon &= -5 \, \text{V} \end{aligned}$$
Loop 3:
$$\begin{aligned} 12 + \epsilon &= Ir + 1 \\ Ir &= 6 \, \text{V} \end{aligned}$$
Using the current information in the diagram,
$$\begin{aligned} I &= 1 + 2 \\ &= 3 \, \text{A} \end{aligned}$$
$$r = 2 \, \Omega$$
$$\begin{aligned}P_{12} &= IV \\ &= 3 (12) \\ &= 36 \, \text{W} \end{aligned}$$
$$P_{\epsilon} = -5 \, \text{W}$$
$$\begin{aligned} P_{r} &= I^{2}r \\ &= 18 \, \text{W} \end{aligned}$$
$$P_{1 \Omega} = 1 \, \text{W}$$
$$P_{3 \Omega} = 12 \, \text{W}$$