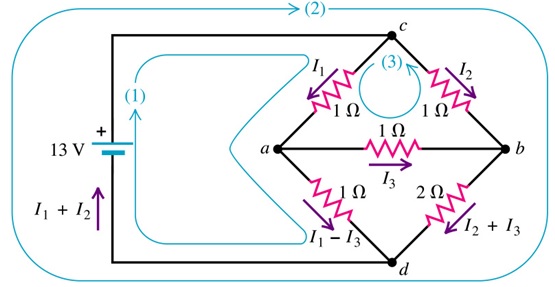
The picture above shows a “bridge” circuit. Find the current in each resistor and the equivalent resistance of the network of five resistors. Find the potential difference $V_{ab}$
Loop 1:
$$\begin{aligned} 13 &= I_{1} + (I_{1} – I_{3}) \\ 2 I_{1} – I_{3} &= 13 \end{aligned}$$
Loop 2:
$$\begin{aligned} 13 &= I_{2} + 2(I_{2} + I_{3}) \\ 3 I_{2} + 2I_{3} &= 13 \end{aligned}$$
Loop 3:
$$\begin{aligned} 0 &= -I_{1} – I_{3} + I_{2} \\ I_{1} – I_{2}&=- I_{3} \end{aligned}$$
Solving the above equations:
$$\begin{aligned} I_{1} &= 6 \, \text{A} \\ I_{2} &= 5 \, \text{A} \\ I_{3} &= -1 \, \text{A} \\ R_{eq} &= \frac{13}{11} \, \Omega \end{aligned}$$