Table of Contents
Momentum (Or Linear Momentum)
Linear momentum is a foundational concept in physics, encapsulating an object’s motion and its intrinsic characteristics.
Linear momentum of an object is a measure of its motion, combining both its mass and its velocity. It is a vector quantity, denoted by $\vec{p}$, and is defined as the product of an object’s mass $m$ and its velocity $\vec{v}$.
Mathematically, this relationship is expressed as:
$$\vec{p} = m\vec{v}$$
, where $m$ represents the mass of the object, and $\vec{v}$ represents its velocity vector.
The direction of the momentum vector is the same as the direction of the velocity vector, indicating that momentum not only quantifies motion but also specifies its direction.
The SI unit of momentum is $\text{kg m s}^{-1}$ or $\text{N s}$.
The more momentum an object has, the harder it is to stop and the greater effect or impact it will experience if it is brought to rest.
Components of Linear Momentum
In three-dimensional space, the motion of an object can be described using rectangular coordinates: $x$, $y$, and $z$. Accordingly, the momentum vector can be decomposed into its components along these axes:
- $p_x = mv_x$
- $p_y = mv_y$
- $p_z = mv_z$
Where $v_x$, $v_y$, and $v_z$ are the components of the velocity vector along the $x$, $y$, and $z$ axes, respectively. This decomposition allows for a more detailed analysis of an object’s motion in three-dimensional space.
Conservation of Momentum
Conservation of momentum states that in a closed system, where no external forces are acting, the total linear momentum remains constant over time. This principle is especially useful in analyzing collisions and interactions between objects, where the total momentum before the interaction equals the total momentum afterward.
To mathematically articulate this principle for an isolated system of particles, where external forces are absent, we can represent this through a series of equations:
- The sum of external forces $\sum \vec{F}$ acting on the system equals zero, indicating no external influence on the system’s momentum.
$$\sum \vec{F} = 0$$ - Consequently, the rate of change of the system’s total momentum $\sum \frac{d \vec{p}}{dt}$ over time is also zero, signifying the momentum’s constancy.
$$\sum \frac{d \vec{p}}{dt} = 0$$ - This leads to the conclusion that the system’s total momentum $\sum \vec{p}$ remains constant.
$$\sum \vec{p} = \text{constant}$$ - Therefore, the total initial momentum of the system $\sum \vec{p}_{i}$ is equal to its total final momentum $\sum \vec{p}_{f}$ after any interactions within the system.
$$\sum \vec{p}_{i} = \sum \vec{p}_{f}$$
This principle is especially invaluable in understanding and predicting the outcomes of complex interactions, such as in collisions where it facilitates the calculation of post-collision velocities and directions.
In simple English:
The total momentum of an isolated system at all times equals its initial momentum.
The total momentum of an isolated system remains constant if there are no external forces present.
Newton’s Second Law Restated In Terms Of Momentum
Newton’s Second Law Of Motion can be applied to relate an applied force to a change of momentum.
Since acceleration, $a = \frac{\Delta v}{\Delta t}$ and assuming that $m$ is a constant,
$$\begin{aligned} F &= ma \\ &= \frac{m \Delta v}{\Delta t} \\ &= \frac{\Delta \left( mv \right)}{\Delta t} \\ F \Delta t &= \Delta \left( mv \right) \end{aligned}$$
or:
$$F \Delta t = \Delta \left( mv_{2}-mv_{1} \right)$$
,where
$v_2$ is the velocity after a force was applied;
$v_1$ is the velocity before the force was applied.
$F \Delta t$ is termed as the impulse.
You can also restate the above as:
$$F = \frac{\Delta \left( mv \right)}{\Delta t}$$
or simply,
$$\vec{F} = \frac{d \vec{p}}{dt}$$
The above equation states that the time rate of change of linear momentum of a particle is equal to the resultant force acting on the particle.
Knowing that the change in momentum caused by a force is useful in solving some problems.
[Optional] What If The Force Varies In Time? – Further Exploration of $\vec{F} = \frac{d \vec{p}}{dt}$
Assume that a single force $\vec{F}$ acts on a particle and that this force varies with time.
$$\begin{aligned} \vec{F} &= \frac{d\vec{p}}{dt} \\ d \vec{p} &= \vec{F} \, dt \end{aligned}$$
Integrating the above, we have:
$$\begin{aligned} \int \, d\vec{p} &= \int \vec{F} \, dt \\ \Delta \vec{p} &= \int\limits_{t_{i}}^{t_{f}} \vec{F} \, dt \\ \vec{p}_{f}-\vec{p}_{i} &= \int\limits_{t_{i}}^{t_{f}} \vec{F} \, dt \end{aligned}$$
Impulse
The impulse of a force $\vec{F}\left( t \right)$ acting on a particle from time $t_{i}$ to $t_{f}$ is:
$$\vec{J} = \vec{p}_{f}-\vec{p}_{i} = \int\limits_{t_{i}}^{t_{f}} \vec{F} \, dt$$
Impulse of a force $\vec{F}$ acting on a particle equals the change in momentum of the particle caused by that force.
Impulse is a vector quantity and has the same dimensions as momentum $\left( \frac{\text{ML}}{\text{T}} \right)$.
The SI unit of impulse is $\text{kg m s}^{-1}$ or $\text{N s}$.
[Optional] Impulsive Force
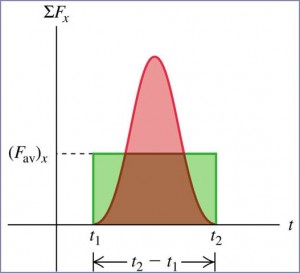
Consider a non-constant force acting on an object, we can find the impulse by find the average force, $\vec{F}_{av}$:
$$\vec{F}_{av} = \frac{1}{\Delta t} \int\limits_{t_{1}}^{t_{2}} \left( \sum \vec{F} \right) \, dt$$
Hence, we have:
$$\begin{aligned} \vec{J} &= \Delta \vec{p} \\ &= \left( \vec{F}_{av} \right) \left( t_{2}-t_{1} \right) \\ &= \vec{F}_{av} \Delta t \end{aligned}$$
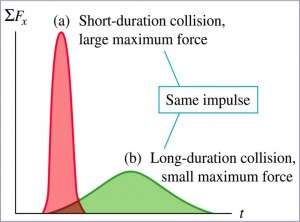
We can use impulse approximation to solve problems. We assume that the impulsive force acts for a short time but is much larger than any other force present and very little motion takes place during this time. (Usually also neglect effects of external forces during this time)
Using $\vec{p}_{i}$ and $\vec{p}_{f}$ to represent the momenta immediately before and after the collision. The impulse, $\vec{p}_{f}-\vec{p}_{i}$ is the same if the area under the $F-t$ curves are the same. The impulsive force is bigger if it acts over a short time and is smaller if it acts over a longer time.
Impulse-Momentum Theorem
The impulse-momentum theorem is a fundamental principle in classical mechanics that relates the impulse applied to an object to the resulting change in its momentum.
The impulse is defined as the product of the average force $\langle F \rangle$ acting on an object and the time $\Delta t$ over which the force is applied.
Mathematically, the impulse $J$ is given by:
$$J = \langle F \rangle \Delta t$$
The impulse-momentum theorem then states that this impulse is equal to the change in momentum $\Delta p$ of the object:
$$J = \Delta p$$
Mathematically, this relationship can be expressed as:
$$\langle F \rangle \Delta t = \Delta p$$
Here are the key terms and definitions:
- Impulse $J$: Impulse is the product of the average force and the time over which it is applied. It is a vector quantity and is given by $J = \langle F \rangle \Delta t$.
- Momentum $p$: Momentum is the product of an object’s mass $m$ and its velocity $v$. It is also a vector quantity. Mathematically, momentum is given by $p = mv$.
- Change in Momentum $\Delta p$: The change in momentum of an object is the difference between its final momentum $p_f$ and initial momentum $p_i$. Mathematically, $\Delta p = p_f-p_i$.
The impulse-momentum theorem is particularly useful when dealing with situations where forces are applied over a certain period of time. It provides a way to quantify how the motion of an object changes in response to applied forces.
The equation $\langle F \rangle \Delta t = \Delta p$ emphasizes that the product of the average force and the time over which it acts is equal to the change in momentum. This theorem is derived from Newton’s second law and is applicable to a wide range of physical scenarios, providing insights into the dynamics of objects subjected to forces.
Kinetic Energy Restated In Terms Of Momentum
In the study of physics, particularly when examining the dynamics of moving objects, momentum and kinetic energy emerge as fundamental concepts. Despite their differences in nature, they are interconnected through several equations that reveal the deeper relationship between motion and energy.
Kinetic energy, denoted as $E_k$, quantifies the energy an object has due to its motion. It is given by the equation:
$$E_k = \frac{1}{2} mv^2$$
By rearranging the terms, kinetic energy can also be represented as:
$$E_k = \frac{m^2v^2}{2m}$$
This simplifies to:
$$E_k = \frac{p^2}{2m}$$
This equation establishes a direct relationship between kinetic energy and the square of momentum, divided by twice the mass of the object.
Vector Nature Of Momentum And The Scalar Nature Of Kinetic Energy
It is crucial to distinguish between the vector nature of momentum and the scalar nature of kinetic energy. Momentum’s vector quality means it has a direction associated with its magnitude; for example, momentum can be positive in one direction (e.g., to the right) and negative in the opposite direction (e.g., to the left). This directional attribute is vital in solving problems involving collisions and motions in multiple dimensions.
Conversely, kinetic energy, being a scalar quantity, lacks direction. Its value is solely dependent on the magnitude of the velocity squared, making it independent of the direction of motion. This distinction is highlighted when calculating the kinetic energy of an object moving in different directions:
- To the right: $E_k = \frac{(+p)^2}{2m} = \frac{p^2}{2m}$
- To the left: $E_k = \frac{(-p)^2}{2m} = \frac{p^2}{2m}$
This symmetry indicates that the kinetic energy of an object is the same regardless of the direction of its motion. The squaring of the momentum vector to calculate kinetic energy effectively converts it into a scalar quantity, emphasizing that the kinetic energy depends only on the speed of the object, not its direction.
Applications of Momentum
The concept of momentum finds extensive application in various areas of physics, including but not limited to:
- Collisions: In studying collisions between objects, whether elastic or inelastic, momentum conservation plays a crucial role in predicting the final states of the objects involved.
- Rocket Propulsion: The principle of conservation of momentum underlies the operation of rockets. As the rocket expels exhaust gases backward, it gains forward momentum, illustrating Newton’s third law of motion.
- Sports Physics: The analysis of motions in sports, such as the impact of a bat on a ball, can be understood through the principles of momentum.
Worked Examples
Example 1
A steady stream of balls, each of mass 0.40 kg and speed 15 ms-1, hits a vertical wall at right angles. After hitting the wall, the balls rebound with the same speed.
Given that 600 balls hit the wall every 10 seconds, calculate the average force acting on the wall. (You may assume that the incident and rebounded balls do not collide.)
- 0 N
- 120 N
- 360 N
- 720 N
Click here to show/hide answer
$$\begin{aligned} \left< F \right> &= N \frac{d \left( mv \right)}{dt} \\ &= \frac{600 \left( 0.40 \right) \left(-15-15 \right)}{10} \\ &=-720 \, \text{N} \end{aligned}$$
is the average force acting on the balls by the wall. By Newton’s 3rd law, the average force acting on the wall is 720N.
Answer: 4
Example 2
a) State Newton’s second law of motion.
b) A 80.0 kg man is parachuting and experiencing a downward acceleration of 2.5 m s-2. The mass of the parachute is 10.0 kg. Calculate the upward force exerted on the system (parachute and man) by the air.
c) Upon reaching the ground, the man uses a pellet gun and fires one pellet per second with a speed of 483 m s-1 perpendicularly onto a wall. The pellet is stopped by the wall and the mass of each pellet is 2.14 g.
i) Find the initial momentum of each pellet.
ii) If each pellet is in contact with the wall for 1.25 ms, calculate the average force exerted on the wall by each pellet while in contact.
iii) Discuss qualitatively, what happens to the average force exerted on the wall by each pellet while in contact if the contact time is increased.
Click here to show/hide answer
a) Newton’s second law of motion states that the rate of change of momentum of a body is directly proportional to the net external force on the body, and the change in momentum is in the direction of the force.
b) By Newton’s second law of motion,
$$\begin{aligned} W – F = ma \\ (80 + 10)(9.81) – F &= (80 + 10.0)(2.5) \\ F &= (80 + 10.0)(9.81 – 2.5) \\ &= 657.9 \\ &= 660 \text{ N} \end{aligned}$$
c)
i)
$$\begin{aligned} \text{Initial momentum} &= mv \\ &= 2.14 \times 10^{-3} \times 483 \\ &= 1.0 \text{ kg m s}^{-1} \end{aligned}$$
ii) By Newton’s second law of motion,
$$\begin{aligned} \text{Force on each bullet by wall} &= \frac{0–1.033}{1.25 \times 10^{-3}} \\ &= -826.896 \text{ N} \end{aligned}$$
By Newton’s third law of motion,
$$\begin{aligned} \text{Force on wall by each pellet} &= 826.896 \text{ N} \\ &= 830 \text{ N} \end{aligned}$$
iii) According to Newton’s second law of motion, if contact time is increased, the average force exerted on the wall by each pellet while in contact will decrease.
Example 3
(a) A man throws a ball of mass 3.0kg with a speed of 5.0 ms-1. If his hand is in contact with the ball for a time interval of 0.20 s while throwing the ball, find the average force he exerts on the ball.
(b) If the man throws 4 balls in 2 seconds, find the average force exerted by him in one second.
(c) If the balls thrown by the man hit a wall and bounce back with speed 3.0 ms-1, find the average force exerted by the wall on the balls.
Click here to show/hide answer
(a)
$$ \begin{aligned} \langle F \rangle &= \frac{\Delta p}{\Delta t} \\ &= \frac{(3)(5)}{0.20} \\ &= 75 \, \text{N} \end{aligned}$$
(b)
$$\begin{aligned} \langle F \rangle \langle t \rangle &= \text{Δ in momentum in one collision} \times \text{collision frequency} \\ \langle F \rangle \times 1 &= 3.0 (5.0-0) \times \left(\frac{4}{2}\right) \\ \langle F \rangle &= 30 \, \text{N} \end{aligned}$$
(c)
$$\begin{aligned} \Delta \text{ in momentum of ball per collision} &= 3.0 (-3.0-5.0) \\ &= -24 \, \text{kg m s}^{-1} \end{aligned}$$
$$\begin{aligned} \langle F \rangle &= -24 \times \left(\frac{4}{2}\right) \\ &= -48 \, \text{N} \end{aligned}$$
Average force exerted by the wall on the ball is $48 \, \text{N}$.
Example 4: Calculating Momentum Components
A drone with a mass of 1.5 kg is flying through a three-dimensional space. Its velocity components are given as $v_x = 5\, \text{m/s}$, $v_y = -3\, \text{m/s}$, and $v_z = 2\, \text{m/s}$. Calculate the components of the drone’s linear momentum in the $x$, $y$, and $z$ directions.
Click here to show/hide answer
To find the components of the drone’s linear momentum, we use the formula for each directional component: $p_x = mv_x$, $p_y = mv_y$, and $p_z = mv_z$.
- For $x$-direction: $p_x = 1.5 \times 5 = 7.5\, \text{kg m/s}$
- For $y$-direction: $p_y = 1.5 \times (-3) = -4.5\, \text{kg m/s}$
- For $z$-direction: $p_z = 1.5 \times 2 = 3\, \text{kg m/s}$
Therefore, the components of the drone’s momentum are $7.5\, \text{kg m/s}$ in the $x$-direction, $-4.5\, \text{kg m/s}$ in the $y$-direction, and $3\, \text{kg m/s}$ in the $z$-direction.
Example 5: Catching a Baseball
A baseball $\text{mass} = 145 g$ is moving toward a catcher at 40 m/s. The catcher catches the ball and brings it to rest in 0.05 seconds. Calculate the average force applied by the catcher’s glove on the ball during this interval.
Click here to show/hide answer
First, convert the mass of the baseball to kilograms: $145 \, \text{g} = 0.145 \, \text{kg}$.
The initial velocity of the ball is $v_i = 40 \, \text{m/s}$, and the final velocity $v_f = 0 \, \text{m/s}$ since the ball comes to rest.
The change in velocity $\Delta v = v_f-v_i = -40 \, \text{m/s}$.
The change in momentum $\Delta p = m \Delta v = 0.145 \, \text{kg} \times -40 \, \text{m/s} = -5.8 \, \text{kg m/s}$.
The time interval $\Delta t = 0.05 \, \text{s}$.
Using the impulse-momentum theorem, $J = \Delta p = -5.8 \, \text{kg m/s}$.
Since $J = \langle F \rangle \Delta t$, the average force $\langle F \rangle = \frac{J}{\Delta t} = \frac{-5.8}{0.05} = -116 \, \text{N}$.
The negative sign indicates the force is applied in the opposite direction of the ball’s initial motion.
Example 6: Rocket Propulsion
A rocket with an initial mass of 2,000 kg (including fuel) ejects fuel at a rate of 5 kg/s with an exhaust velocity of 750 m/s relative to the rocket. Calculate the average force exerted by the expelled fuel if the fuel is ejected continuously for 2 seconds.
Click here to show/hide answer
The momentum of the expelled fuel per second is given by the product of the rate of mass ejection and the exhaust velocity,
$$\Delta p = 5 \, \text{kg/s} \times 750 \, \text{m/s} = 3750 \, \text{kg m/s}^2$$
Over 2 seconds, the total change in momentum
$$J = 3750 \, \text{kg m/s}^2 \times 2 = 7500 \, \text{kg m/s}$$
The impulse-momentum theorem states $J = \langle F \rangle \Delta t$, so the average force
$$\langle F \rangle = \frac{J}{\Delta t} = \frac{7500}{2} = 3750 \, \text{N}$$
This force is directed opposite to the exhaust velocity, propelling the rocket forward.
Example 7: Swinging a Golf Club
A golf club hits a golf ball $\text{mass} = 45.93 g$ and accelerates it from rest to a speed of 70 m/s in 0.002 seconds. Calculate the average force exerted on the ball by the golf club during the impact.
Click here to show/hide answer
Convert the mass of the golf ball to kilograms:
$$45.93 \, \text{g} = 0.04593 \, \text{kg}$$
The change in velocity $\Delta v = 70 \, \text{m/s}$ since the initial velocity is 0.
The change in momentum $\Delta p = m \Delta v = 0.04593 \, \text{kg} \times 70 \, \text{m/s} = 3.2151 \, \text{kg m/s}$.
The time interval $\Delta t = 0.002 \, \text{s}$.
Using the impulse-momentum theorem, $J = \Delta p = 3.2151 \, \text{kg m/s}$.
Thus, the average force
$$\langle F \rangle = \frac{J}{\Delta t} = \frac{3.2151}{0.002} = 1607.55 \, \text{N}$$
, indicating a very high force applied over a very short interval.
Example 8: Crumple Zones in Cars
Background: Crumple zones are designed into vehicles to absorb the impact energy during a collision, thereby reducing the force experienced by the occupants. They work by increasing the time over which the collision occurs, which according to the impulse-momentum theorem, reduces the average force exerted on the vehicle (and thus its occupants) during impact.
Scenario: A car with a mass of 1,500 kg is traveling at 20 m/s (about 72 km/h) when it hits a stationary obstacle. Thanks to its crumple zones, the car decelerates uniformly to a halt over a distance of 1 meter. Without the crumple zones, the same car would come to a halt over a distance of just 0.5 meters.
Part A: Calculate the average force exerted on the car during the collision when the crumple zones are effectively utilized (deceleration distance = 1 m).
Part B: Calculate the average force exerted on the car during the collision when the crumple zones are not utilized (deceleration distance = 0.5 meters).
Part C: Discuss why crumple zones are vital for passenger safety during collisions, based on your calculations from Parts A and B.
Click here to show/hide answer
Part A:
Given:
- Mass of car, $m = 1500 \, \text{kg}$
- Initial velocity, $v_i = 20 \, \text{m/s}$
- Final velocity, $v_f = 0 \, \text{m/s}$ (since the car comes to a halt)
- Deceleration distance with crumple zones, $d = 1 \, \text{m}$
Initial kinetic energy ($KE_i$):
$$\begin{aligned} KE_i &= \frac{1}{2} \times 1500 \, \text{kg} \times (20 \, \text{m/s})^2 \\ &= \frac{1}{2} \times 1500 \times 400 \\ &= 300,000 \, \text{J} \end{aligned}$$
Final kinetic energy ($KE_f$) is 0 because the car stops.
Change in kinetic energy ($W$) is $300,000 \, \text{J}$ (since $KE_f-KE_i = -300,000 \, \text{J}$, and work done is equal to this change in energy).
Average force with crumple zones ($F$) is:
$$F = \frac{W}{d} = \frac{300,000 \, \text{J}}{1 \, \text{m}} = 300,000 \, \text{N}$$
Part B:
Using a deceleration distance of $0.5 \, \text{m}$:
$$F = \frac{300,000 \, \text{J}}{0.5 \, \text{m}} = 600,000 \, \text{N}$$
Part C:
The calculations from Parts A and B illustrate the importance of crumple zones. With crumple zones, the average force during a collision is significantly reduced (from 600,000 N without crumple zones to 300,000 N with crumple zones). This reduction in force is crucial for passenger safety, as it lowers the risk of injury. Crumple zones achieve this by increasing the time over which the collision occurs, which, according to the impulse-momentum theorem, decreases the average force exerted during the impact. This example underscores the role of physics and engineering in designing safer vehicles.
Example 9
Utilize the concepts of impulse and change in momentum to explain the following:
a) Explain the reason for flexing your legs when leaping from a wall to the ground.
b) Discuss the purpose of hockey players donning shin pads for leg safeguarding.
c) Describe the rationale behind retracting your hands when catching a swiftly approaching ball.
Click here to show/hide answer
a) Flexing Your Legs When Leaping from a Wall to the Ground
When you leap from a wall to the ground and flex your legs upon landing, you are essentially increasing the time over which the collision (landing) occurs. The impulse experienced by your body is equal to the change in momentum, given by the formula:
$$\text{Impulse} = \Delta p = F \Delta t$$
where $\Delta p$ is the change in momentum, $F$ is the average force exerted during the collision, and $\Delta t$ is the time over which the force is applied. By flexing your legs, you increase $\Delta t$, the time over which your momentum changes from a high downward momentum to zero. According to the formula, if $\Delta t$ is larger, the force $F$ you experience (which equates to the force your legs need to exert to stop your fall) is reduced. This reduction in force decreases the risk of injury, as the bones, muscles, and joints absorb less impact force.
b) Hockey Players Donning Shin Pads for Leg Safeguarding
Hockey players wear shin pads to protect their legs from the high-impact forces of flying hockey pucks and sticks. The shin pads serve to distribute the force of the impact over a larger area and increase the time over which the impact occurs. This is another application of the impulse-momentum theorem. When a hockey puck strikes a shin pad, the pad compresses and deforms, increasing the duration of the impact ($\Delta t$) compared to what it would be if the puck hit the bare skin and bone directly. By increasing $\Delta t$, the average force $F$ transmitted to the player’s leg is significantly reduced. This minimizes the risk of fractures or severe bruising, thereby safeguarding the player’s legs effectively.
c) Retracting Your Hands When Catching a Swiftly Approaching Ball
Retracting your hands when catching a ball that is moving towards you fast increases the time over which the ball’s momentum is brought to zero. Just like in the previous examples, this action relates to the impulse-momentum theorem. The initial momentum of the ball is significant due to its high velocity. By moving your hands backward upon catching the ball, you increase the time duration $\Delta t$ over which the ball’s momentum decreases to zero. This increase in $\Delta t$ results in a decrease in the average impact force $F$ on your hands. The reduction in force makes the catch less painful and reduces the likelihood of injury. It also increases the chance of successfully catching the ball without it bouncing off your hands, as the softer catch (due to lower force) helps in absorbing the ball’s momentum more effectively.