Table of Contents
Step-By-Step Guide For Derivation Of Moment Of Inertia Of A Thin Spherical Shell
A thin uniform spherical shell has a radius of R and mass M. Calculate its moment of inertia about any axis through its centre.
Moment Of Inertia Of A Thin Spherical Shell is:
$$I = \frac{2}{3} MR^{2}$$
Note: If you are lost at any point, please visit the beginner’s lesson (Calculation of moment of inertia of uniform rigid rod) or comment below.
Outline Of Solution
This solution presents a detailed walkthrough for calculating the moment of inertia of a thin uniform spherical shell about any axis through its centre. The approach is methodical, breaking down complex concepts into manageable steps for better understanding. Whether this is your first time dealing with such problems or you’re looking for a refresher, this guide aims to clarify the process comprehensively.
Step 1: Conceptualizing the Problem
- Understanding the Shell: View the spherical shell as a collection of thin circular hoops, uniformly distributed across the shell’s surface. This perspective simplifies the problem by allowing us to consider the moment of inertia of simpler shapes (circular hoops) and then integrating these to find the total moment of inertia for the shell.
- Axis of Rotation: Our focus is on calculating the moment of inertia about an axis that passes through the centre of the spherical shell. This central axis is crucial because it allows for a symmetrical analysis of the shell’s mass distribution relative to the axis.
Step 2: Dividing the Shell into Elements
- Slicing the Shell: Imagine dissecting the spherical shell into an infinite number of thin circular hoops. This conceptual step is vital for applying calculus to determine the shell’s moment of inertia, as it breaks down the complex shape into manageable elements.
- Area and Mass of a Hoop: Each thin hoop’s mass ($dm$) is a fraction of the shell’s total mass ($M$), related to the hoop’s surface area ($dA$). This relation is fundamental to deriving an expression for the mass of each hoop, which is crucial for calculating the moment of inertia.
Step 3: Mathematical Formulation
- Expressing $dm$ and $dA$: We derive expressions for the mass ($dm$) of a hoop and its surface area ($dA$) using the shell’s total surface area and the geometry of the hoops. This step involves understanding the relationship between the hoop’s radius ($r$), its circumference, and the spherical shell’s radius ($R$).
- Moment of Inertia of a Hoop: The moment of inertia ($dI$) for each hoop is expressed as $r^2 \: dm$, incorporating the hoop’s radius and differential mass. This formula is pivotal for integrating the contributions of all hoops to find the shell’s total moment of inertia.
Step 4: Integrating Over the Shell
- Setting Up the Integral: With the expressions for $dm$ and $dI$ established, we integrate over the spherical shell’s surface to calculate the total moment of inertia ($I$). This step involves integrating $dI$ across all possible values of $\theta$, from $0$ to $\pi$, to account for every hoop making up the shell.
- Integration Process: This phase delves into the technicalities of integrating the moment of inertia expression, requiring an understanding of trigonometric identities and substitution methods to solve the integral.
Step 5: Final Calculation
- Computing $I$: The culmination of this process is the integration of the moment of inertia formula, resulting in the final expression for the moment of inertia of a thin uniform spherical shell about any axis through its centre: $I = \frac{2}{3} MR^2$.
Conclusion
This structured approach combines physical insights into the geometry of a spherical shell with mathematical techniques from calculus. By breaking down the shell into infinitesimally small hoops, calculating the moment of inertia for each, and integrating these contributions, we obtain a comprehensive solution. This method not only elucidates the specific problem of the spherical shell’s moment of inertia but also illustrates the power of calculus in solving complex physical problems.
Full Derivation Of Moment Of Inertia Of A Thin Spherical Shell
Understanding the Structure
The Spherical Shell: Imagine a thin spherical shell as a collection of numerous thin circular hoops, each contributing to the shell’s overall mass and structure.
Fundamental Principle: Recall from our study on the moment of inertia for a cylinder, the moment of inertia for a thin circular hoop is given by $I = Mr^2$. This principle forms the foundation of our calculations.
Main Article: Derivation Of Moment Of Inertia Of A Hollow/Solid Cylinder
Deriving the Differential Moment of Inertia
Equation Basis: Starting with the fundamental equation for a hoop’s moment of inertia, we express the differential moment of inertia ($dI$) as a function of the differential mass ($dm$) and the radius ($r$):
$$ \begin{equation} dI = r^{2} \, dm \end{equation} \tag{1}$$
Mass Element ($dm$) Expression: To progress, it’s essential to establish a formula for $dm$, which is directly related to the shell’s surface area ($A$):
$$\begin{aligned} dm &= \frac{M}{A} \, dA \end{aligned} \tag{2} $$
Here, $A$ represents the total surface area of the shell, which is $4 \pi R^2$.
Calculating the Differential Area ($dA$)
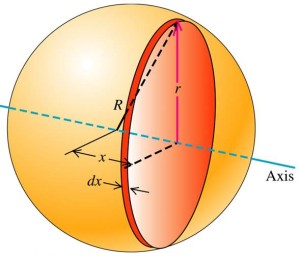
Conceptualizing $dA$: If $A$ is the total surface area of the shell, $dA$ is the area of one of the many thin circular hoops. With reference to the picture, each thin circular hoops can be thought to be a thin rectangular strip. Hence, the differential area ($dA$) of a hoop is akin to a thin rectangular strip, calculated as the product of its length (the hoop’s circumference) and breadth (arc length, $dx$), where the normal arc length equation $R \theta$ is applicable.
$$\begin{aligned} dA &= \text{length} \times \text{breadth} \\ &= \text{circumference} \times \text{arc length} \\ &= 2 \pi r \times R \: d \theta \end{aligned} \tag{3}$$
Now, in Equation 3, notice that you will have different $r$ for different hoops (i.e. the radius ($r$) varies for different hoops). Hence, we have to find a way to relate $r$ with $\theta$.
Relating $r$ With $\theta$
Consider the above picture, notice that there is a right-angle triangle with angle $\theta$ formed at the shell’s center, we find:
$$ \sin \theta = \frac{r}{R}$$
$$r = R \, \sin \theta \tag{4}$$
Implementing Substitutions
With the relationship between $r$ and $\theta$ established in Equation 4, $dA$ in Equation 3 simplifies to:
$$dA = 2 \pi R^{2} \sin \theta \: d \theta \tag{5}$$
Substituting the Equation 5 into our mass element $dm$ equation – Equation 2, we have:
$$dm = \frac{M \sin \theta}{2} d \theta \tag{6}$$
Substituting Equation 6 and the Equation 4 into Equation 1, we have:
$$\begin{aligned} dI &= r^{2} \: dm \\ &= (R \sin \theta)^{2} \frac{M \sin \theta}{2} \: d \theta \\ &= \frac{MR^{2}}{2} \sin^{3} \theta \: d \theta \end{aligned}$$
Integration
Integrating for $I$: Through integration from $0$ to $\pi$, we calculate the total moment of inertia:
$$I = \frac{M R^{2}}{2} \int\limits_{0}^{\pi} \sin^{3}{\theta} \: d \theta$$
For those who knows how to integrate $\sin^{3}{\theta}$, you’re done with this post. For those who needs a little bit more help, read on.
Now, we split the $\sin^{3}{\theta}$ into two,
$$I = \frac{M R^{2}}{2} \int\limits_{0}^{\pi} \sin^{2}{\theta} \: \sin{\theta} \: d \theta$$
From the trigonometric identity $\sin^{2} \theta = 1-\cos^{2} \theta$, we have:
$$I = \frac{M R^{2}}{2} \int\limits_{0}^{\pi} (1-\cos^{2}{\theta}) \: \sin{\theta} \: d \theta$$
Now, at this point, we will use the substitution: $u = \cos{\theta}$. By substituting $u = \cos{\theta}$, we also change the differential $d\theta$ to $du$. Since $d\theta = \frac{du}{- \sin{\theta}} \rightarrow \sin \theta \: d\theta = -du$, and $u = \cos{\theta}$, we adjust the integral limits based on the substitution:
- At $\theta = 0$, $u = \cos{0} = 1$.
- At $\theta = \pi$, $u = \cos{\pi} = -1$.
Therefore, the integral becomes:
$$I = \frac{MR^{2}}{2} \int\limits_{1}^{-1} (u^{2}-1) \, du \tag{7}$$
For those who knows how to integrate from here, you are done with this post. For those who needs a little bit more help, read on. Since we’re integrating $u^2 – 1$, let’s expand and integrate term by term:
$$\int (u^2-1) \, du = \frac{u^3}{3}-u$$
Evaluating this from (1) to (-1):
$$= \left[ \frac{u^3}{3}-u \right]_{1}^{-1}$$
$$= \left( \frac{(-1)^3}{3}-(-1) \right) – \left( \frac{1^3}{3}-1 \right)$$
$$= \left( -\frac{1}{3} + 1 \right)-\left( \frac{1}{3}-1 \right)$$
$$= -\frac{1}{3} + 1-\frac{1}{3} + 1$$
$$= \frac{2}{3} + \frac{2}{3}$$
$$= \frac{4}{3}$$
Final Result
Putting the result of $\frac{4}{3}$ back into Equation 7, we get the final result:
$$I = \frac{2}{3} MR^{2} \tag{8}$$
We’re done!
Derivation Of Moment Of Inertia Of Other Common Shapes
- Uniform Rigid Rod (“Beginners’ Lesson”)
- Hollow/solid Cylinder
- Uniform Solid Sphere