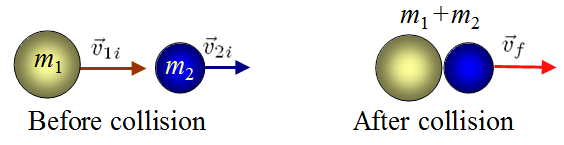Table of Contents
Collision
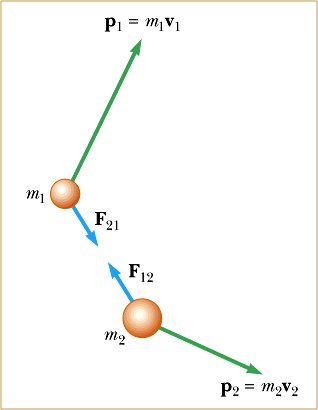
In a collision, two particles come together for a short time and thereby produce impulsive forces on each other.
Remember that all forces are field forces when viewed at small enough scale.
Even an object in space pulled around by the gravitational forces of the planets or Sun may be considered as collisions.
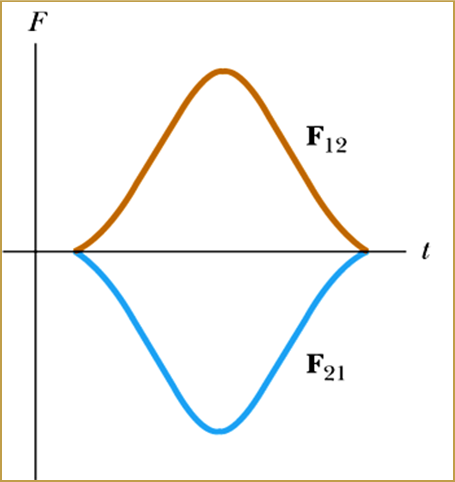
Consider two objects with mass $m_{1}$ and $m_{2}$ undergoing a collision. During the collision, they will exert a force on each other, as given by $\vec{F}_{12}$ and $\vec{F}_{21}$. The forces will vary according to the graph given below:
Hence, the total change in momentum for object 1 with mass $m_{1}$ is:
$$\Delta \vec{p}_{1} = \int\limits_{t_{i}}^{t_{f}} \vec{F}_{21} \, dt$$
For object 2 with mass $m_{2}$:
$$\Delta \vec{p}_{2} = \int\limits_{t_{i}}^{t_{f}} \vec{F}_{12} \, dt$$
From Newton’s Third Law,
$$\begin{aligned} \Delta \vec{p}_{2} &=-\Delta \vec{p}_{2} \\ \Delta \vec{p}_{1} + \Delta \vec{p}_{2} &= 0 \\ \vec{p}_{\text{tot}} &= \vec{p}_{1} + \vec{p}_{2} = \text{const.} \end{aligned}$$
Conservation of Momentum
Main article: Momentum
The principal of conservation of momentum states that the total momentum of a system of objects remains constant provided no resultant external force acts on the system.
- It is a direct result from Newton’s Second and Third Laws of Motion.
- It provides a convenient way to calculate some parameters, such as final velocities, in collisions without the need to know the exact forms of the forces involved.
Head-on collisions are one-dimensional collisions, which occur, in the same straight line without any deviations to this original straight path.
Elastic Collision
Elastic collision in which both total momentum and total kinetic energy are conserved.
In an elastic collision, the kinetic energy lost by one body during an elastic collision is transferred to the other body so that the total kinetic energy of the colliding bodies is conserved.
For an elastic collision, it can be shown that the relative speed of approach of the bodies before collision is equal to the relative speed of separation of the bodies after collisions.
Inelastic Collision
Inelastic collision in which total momentum is conserved but total kinetic energy is not conserved.
In inelastic collisions, some of the kinetic energy is converted to heat, sound or some other forms of energy when the objects are deformed after the collision. Therefore, in an inelastic collision, the total kinetic energy is not conserved.
Completely Inelastic Collision
Completely inelastic collision in which total momentum is conserved and the particles stick together after collision so that their final velocities are the same. Total kinetic energy is not conserved.
Momentum & Kinetic Energy in Collisions
The total momentum of the colliding bodies is always conserved in all types of collisions, as long as there is no resultant force acting on the system. However, the momentum of each individual colliding body is not conserved.
When finding the total kinetic energy of the colliding bodies, the direction of travel of bodies is not taken into account since kinetic energy is scalar, unlike the case when we are finding the total momentum (vector).
Note:
- When using the equation of relative velocities for elastic collision, direction of travel of the particle is important.
- If the particles approach towards each other, the relative speed of approach would be the sum of the approaching speeds; if they separate from each other in opposite directions, the relative speed of separation would be the sum of the separating speeds.
Special cases:
For elastic collision of two particles of equal mass, the particles simply exchange their velocities after the collision.
If $u_{2}$ = 0 (particle M originally at rest:
- If m = M (identical particle):
- The two particles exchange velocities
- If m << M:
- m rebounds with almost same speed while M remains stationary.
- If m >>M (a heavy particle hitting a very light particle)
- m continues with same speed, M goes off with twice speed of m.
[Uni Physics] Further Investigation On Elastic & Inelastic Collisions
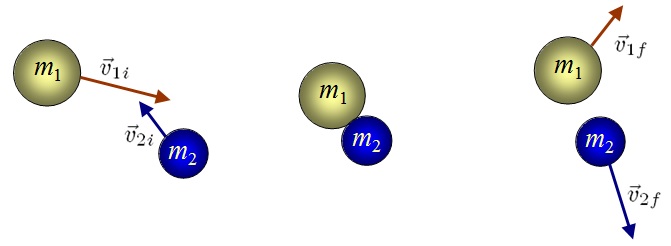
Elastic Collision
Consider the elastic collision as shown in the diagram above.
From momentum conservation:
$$\begin{aligned} \text{Initial Momentum} &= \text{Final Momentum} \\ m_{1}v_{1i} + m_{2}v_{2i} &= m_{1}v_{1f}+m_{2}v_{2f} \end{aligned}$$
From energy conservation:
$$\begin{aligned} \text{Initial Kinetic Energy} &= \text{Final Kinetic Energy} \\ \frac{1}{2}m_{1}v_{1i}^{2} + \frac{1}{2}m_{2}v_{2i}^{2} &= \frac{1}{2} m_{1}v_{1f}^{2} + \frac{1}{2} m_{2} v_{2f}^{2} \end{aligned}$$
Let’s find the final velocities in terms of the initial velocities.
Let’s start with the energy conservation equation,
$$\begin{aligned} \frac{1}{2}m_{1}v_{1i}^{2} + \frac{1}{2}m_{2}v_{2i}^{2} &= \frac{1}{2} m_{1}v_{1f}^{2} + \frac{1}{2} m_{2} v_{2f}^{2} \\ m_{1} \left( v_{1i}^{2}-v_{1f}^{2} \right) &= m_{2} \left( v_{2f}^{2}-v_{2i}^{2} \right) \\ m_{1} \left( v_{1i}-v_{1f} \right) \left( v_{1i} + v_{1f} \right) &= m_{2} \left( v_{2f}-v_{2i} \right) \left( v_{2f} + v_{2i} \right) \, \, – \text{Eqn 1}\end{aligned}$$
From the conservation of momentum equation,
$$\begin{aligned} m_{1}v_{1i} + m_{2}v_{2i} &= m_{1}v_{1f}+m_{2}v_{2f} \\ m_{1} \left( v_{1i}-v_{1f} \right) &= m_{2} \left( v_{2f}-v_{2i} \right) \, \, – \text{Eqn 2} \end{aligned}$$
Dividing Equation 1 by Equation 2, we have:
$$\begin{aligned} v_{1i} + v_{1f} &= v_{2f} + v_{2i} \\ v_{1i}-v_{2i} &= v_{2f}-v_{1f} \, \, – \text{Eqn 3}\end{aligned}$$
Notice that we can get $\frac{v_{2f}-v_{1f}}{v_{1i}-v_{2i}} = 1$ from Equation 3. The fraction $\frac{v_{2f}-v_{1f}}{v_{1i}-v_{2i}}$ is known as the coefficient of restitution, $e$. We will look into that later.
Continuing from Equation 3,
$$\begin{aligned} v_{1i}-v_{2i} &= v_{2f}-v_{1f} \\ v_{2f} &= v_{1i} + v_{1f}-v_{2i} \, \, – \text{Eqn 4} \end{aligned}$$
Sub. Equation 4 into momentum conservation equation – $m_{1}v_{1i} + m_{2}v_{2i} = m_{1}v_{1f} + m_{2}v_{2f}$, we have:
$$\begin{aligned} m_{1}v_{1i} + m_{2}v_{2i} &= m_{1}v_{1f} + m_{2} \left( v_{1i} + v_{1f}-v_{2i} \right) \\ \left( m_{1}-m_{2} \right) v_{1i} + \left( m_{2} + m_{2} \right) v_{2i} &= \left( m_{1} + m_{2} \right) v_{1f} \end{aligned}$$
Making $v_{1f}$ the subject, we obtain:
$$v_{1f} = \left( \frac{m_{1}-m_{2}}{m_{1}+m_{2}} \right) v_{1i} + \left( \frac{2m_{2}}{m_{1}+m_{2}} \right) v_{2i} $$
Using the same method, one can find the final velocity for object 2:
$$v_{2f} = \left( \frac{2m_{1}}{m_{1}+m_{2}} \right) v_{1i} + \left( \frac{m_{2}-m_{1}}{m_{1}+m_{2}} \right) v_{2i}$$
Armed with the result, let’s look at specific cases.
Case 1: If $m_{1} = m_{2}$, we have:
$$\begin{aligned} v_{1f} &= v_{2i} \\ v_{2f} &= v_{1i} \end{aligned}$$
The particles exchange velocities.
Case 2: If $m_{2}$ is initially at rest $\left( v_{2i} = 0 \right)$, then
$$\begin{aligned} v_{1f} &= \left( \frac{m_{1}-m_{2}}{m_{1}+m_{2}} \right) v_{1i} \\ v_{2f} &= \left( \frac{2 m_{1}}{m_{1} + m_{2}} \right) v_{1i} \end{aligned}$$
When $m_{1} \gg m_{2}$, we have $v_{1f} \approx v_{1i}$ and $v_{2f} \approx 2 v_{1i}$.
When $m_{2} \gg m_{1}$, we have $v_{1f} \approx-v_{1i}$ and $v_{2f} \approx 0$.
Transfer Of Kinetic Energy During Elastic Collision
Often, we want to know how much kinetic energy is transferred to a stationary target $\left( v_{2i} = 0 \right)$. Using $v_{2f} = \left( \frac{2 m_{1}}{m_{1} + m_{2}} \right) v_{1i}$, we have
$$\begin{aligned} \text{KE}_{2f} &= \frac{1}{2} m_{2} \left( \frac{2m_{1}}{m_{1}+m_{2}} \right)^{2} v_{1i}^{2} \\ &= \frac{4m_{2}m_{1}}{\left( m_{1} + m_{2} \right)^{2}} \text{KE}_{1i} \end{aligned}$$
Let’s look at two cases,
Case 1: $m_{2} \gg m_{2}$, we have:
$$\text{KE}_{2f} \approx 4 \frac{m_{1}}{m_{2}} \text{KE}_{1i}$$
Case 2: $m_{1} \gg m_{2}$, we have:
$$\text{KE}_{2f} \approx 4 \frac{m_{2}}{m_{1}} \text{KE}_{1i}$$
From the above, you can see that maximum kinetic energy transfer will occur when $m_{1} = m_{2}$
Perfectly (Totally) Inelastic Collisions
In a totally inelastic collision, two particles with masses $m_{1}$ and $m_{2}$ collide head-on and stick together after the collision. The combined particle will move with some common velocity $\vec{v}_{f}$.
From momentum conservation:
$$\begin{aligned} m_{1} \vec{v}_{1i} + m_{2} \vec{v}_{2i} &= \left( m_{1} + m_{2} \right) \vec{v}_{f} \\ \vec{v}_{f} &= \frac{m_{1}\vec{v}_{1i} + m_{2} \vec{v}_{2i}}{m_{1}+m_{2}} \end{aligned}$$
Coefficient Of Restitution
Coefficient of restitution is defined as:
$$\begin{aligned} e &= \frac{\text{Relative speed of separation}}{\text{Relative speed of approach}} \\ &= \frac{v_{2f}-v_{1f}}{v_{1i}-v_{2i}} \end{aligned}$$
For a perfectly inelastic collision, e is 0. For inelastic collision, $e < 1$. For elastic collision, $e > 1$.
2-D Collisions
For 2D collisions, the momentum in each direction is conserved. The conservation equations for the above is:
$$\begin{aligned} m_{1}v_{1ix} + m_{2}v_{2ix} &= m_{1}v_{1fx} + m_{2}v_{2fx} \\ m_{1}v_{1iy}+m_{2}v_{2iy} &= m_{1}v_{1fy} + m_{2} v_{2fy} \end{aligned}$$
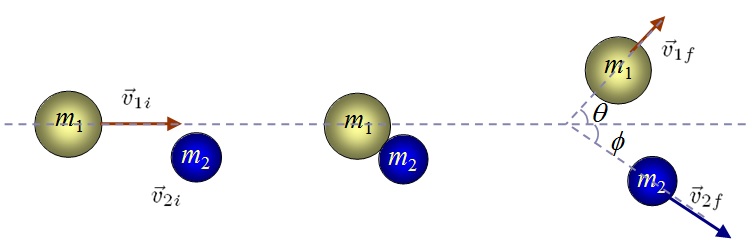
In two dimensions, there are four unknowns, either $v_{1fx}$, $v_{1fy}$, $v_{2fx}$, $v_{2fy}$, or if we use the magnitudes and angles, $v_{1f}$, $v_{2f}$, $\theta$ and $\phi$.
We can only write down two equations for conservation of linear momentum in their component directions.
We may be able to add one more equation relating energy if the collision is perfectly elastic.
We will need at least another parameter to determine the final outcome. The final parameter will be one of the unknowns as stated above.
The exception to this rule will be perfectly inelastic collision. In perfectly inelastic collision, there are only two unknowns and the final outcome is uniquely determined by conservation of linear momentum along.
Elastic Glancing Collision
The diagram above shows the case of elastic glancing collision. From the conservation of momentum, we have:
In the horizontal direction,
$$m_{1}v_{1i} = m_{1}v_{1f} \cos{\theta} + m_{2}v_{2f} \cos{\theta}$$
In the vertical direction,
$$0 = m_{1}v_{1f}\sin{\theta}-m_{2}v_{2f}\sin{\theta}$$
Since it is an elastic collision, the kinetic energy is conserved, which is given by:
$$\frac{1}{2}m_{1}v_{1i}^{2} = \frac{1}{2}m_{1}v_{1f}^{2} + \frac{1}{2}m_{2}v_{2f}^{2}$$
You can analyze the rest of the equations with the same methods that has been shown above. Let’s look at a special case of the elastic glancing collision, whereby $m_{1} = m_{2} = m$.
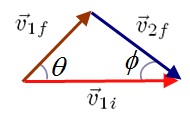
From the conservation of momentum, we have:
$$\vec{v}_{1i} = \vec{v}_{1f} + \vec{v}_{2f}$$
From the conservation of energy, we have:
$$v_{1i}^{2} = v_{1f}^{2} + v_{2f}^{2}$$
From the above 2 equations, we can see that $\vec{v}_{1i}$, $\vec{v}_{1f}$ and $\vec{v}_{2f}$ makes a triangle, as shown by the figure below.
Hence, we can conclude that:
$$\theta + \phi = 90^{\circ}$$
The objects leave each other at a $90^{\circ}$ angle.
Problem Solving Strategy for 2-Dimensional Collision Problems
When dealing with problems involving two-dimensional (2-D) collisions, a systematic approach can significantly simplify the analysis and solution. These events, where objects collide and interact in a plane, require careful consideration of both momentum and energy conservation principles. Here is a step-by-step guide for solving 2-D collision problems effectively:
1. Establishing the Coordinate System
The first step involves setting up an appropriate coordinate system to analyze the problem. It is advantageous to align one axis, typically the x-axis, with the initial velocity vector of one of the objects involved in the collision. This choice can simplify calculations by possibly reducing the number of components that need to be considered. Selecting a suitable coordinate system at the outset is crucial for organizing the problem effectively and can lead to a more straightforward solution process.
2. Visualizing the Scenario
Sketching the scenario is an invaluable step. This involves drawing and labeling all relevant velocity vectors before and after the collision. Include both initial and final velocities for all objects involved. Represent these vectors accurately in your diagram, with their directions and magnitudes (where known). This visual representation can help in understanding the dynamics of the collision and in identifying the relationships between the various quantities involved.
3. Applying the Conservation of Momentum
Momentum conservation is a fundamental principle in collision problems. For 2-D collisions, you must apply the law of conservation of momentum separately in two perpendicular directions, usually aligned with your chosen coordinate system (x and y directions). Write down the momentum conservation equations for each direction:
- In the x-direction: $m_1v_{1x} + m_2v_{2x} = m_1v'{1x} + m_2v'{2x}$
- In the y-direction: $m_1v_{1y} + m_2v_{2y} = m_1v'{1y} + m_2v'{2y}$
where $m_1$ and $m_2$ are the masses of the objects, $v_{1x}, v_{2x}, v_{1y},$ and $v_{2y}$ are the initial velocity components, and $v'{1x}, v'{2x}, v'{1y},$ and $v'{2y}$ are the final velocity components.
4. Considering Energy Conservation
- Elastic Collisions: If the collision is elastic, kinetic energy is conserved. In addition to momentum conservation equations, write down the equation for the conservation of kinetic energy:
$$\frac{1}{2}m_1v_1^2 + \frac{1}{2}m_2v_2^2 = \frac{1}{2}m_1v’^2_1 + \frac{1}{2}m_2v’^2_2$$
This equation can help solve for unknowns when combined with the momentum conservation equations.
- Inelastic Collisions: If the collision is inelastic, kinetic energy is not conserved. For totally inelastic collisions, the objects stick together and have the same final velocity. This condition simplifies the final state and can be directly applied to solve for the final velocities.
5. Incorporating Additional Information
Often, collision problems will include extra information that can be pivotal in finding a solution. This may involve the direction of one of the final velocities, constraints on the motion after the collision, or specific conditions related to the collision’s nature. Carefully integrate this information into your analysis to comprehensively address the problem.
6. Solving the Equations
With all relevant equations and information at hand, proceed to solve the equations. This step may involve algebraic manipulation and possibly the use of systems of equations. The goal is to find the unknown quantities, typically the final velocities of the objects involved. Depending on the complexity of the problem, you may need to employ mathematical software or calculators to assist in solving these equations.
Conclusion
This structured approach to solving 2-D collision problems in physics not only organizes your thought process but also ensures that all physical principles relevant to the problem are considered. By methodically applying these steps, students can effectively analyze and solve complex collision scenarios, enhancing their understanding of momentum and energy conservation in two-dimensional dynamics.
Worked Examples
Example 1
An object of mass 1.5 kg is sliding with a velocity of 3.0 m s-1 on a frictionless surface towards another object which is stationary and has a mass of 2.0 kg. This head-on collision is completely inelastic. If the duration of the collision is 0.050 s, find the average force that is exerted between the objects during the collision.
- 39 N
- 51 N
- 90 N
- 119 N
Click here to show/hide answer
By conservation of momentum,
$$\begin{aligned} m_1u_1 + m_2u_2 &= (m_1 + m_2)v \\ (1.5)(3.0) &= (1.5 + 2.0)v \\ v &= 1.29 \, \text{m s}^{-1} \end{aligned}$$
By Newton’s 2nd Law,
$$\langle F \rangle \Delta t = \Delta p$$
Consider 1.5 kg mass:
$$\begin{aligned} \langle F \rangle (0.050) &= (1.5)(1.29 – 3.0) \\ \langle F \rangle &= -51.3 \, \text{N} \end{aligned}$$
Consider 2.0 kg mass:
$$\begin{aligned} \langle F \rangle (0.050) &= (2.0)(1.29 – 0) \\ \langle F \rangle &= 51.6 \, \text{N} \end{aligned}$$
Answer: 2
Example 2
A lorry and a motorcycle with different masses are involved in a head on collision, after which they travel in the opposite direction. The speeds of the lorry and the motorcycle before the collision are 10.0 m s-1 and 13.0 m s-1 respectively, and after the collision are 5.0 m s-1 and 28.0 m s-1 respectively.
Which of the following statements about the collision is true?
- Motorcycle experienced a larger force than lorry during the collision.
- Magnitudes of impulses experienced by lorry and motorcycle during the collision are the same.
- Individual momentums of lorry and motorcycle are conserved.
- Total kinetic energy of lorry and motorcycle is conserved.
Click here to show/hide answer
To solve this problem, let’s examine each statement based on the principles of physics, particularly the conservation of momentum and the relationship between force, impulse, and changes in momentum.
1. Motorcycle experienced a larger force than lorry during the collision.
The force experienced by an object during a collision relates to the impulse imparted to it, which is the change in momentum $\Delta p$ of the object. The impulse experienced by an object can be calculated as the product of the force and the time over which the force acts $I = F \times t$, and it is also equal to the change in momentum $I = \Delta p$.
Though the question doesn’t provide the masses of the lorry and the motorcycle, the force experienced by each can be inferred from the change in their momentums. However, without knowing the duration of the collision for both vehicles, we cannot directly compare the forces they experienced based solely on the information provided. Still, the principle of Newton’s third law, “For every action, there is an equal and opposite reaction,” suggests that the forces experienced by both would be equal in magnitude and opposite in direction, not necessarily that one experienced a larger force than the other over the duration of the impact.
2. Magnitudes of impulses experienced by lorry and motorcycle during the collision are the same.
This statement is true based on Newton’s third law. The impulse experienced by each object is equal to the change in momentum, and since the forces acting on them are equal in magnitude and opposite in direction for the same duration, the impulses (changes in momentum) they experience will also be equal in magnitude.
3. Individual momentums of lorry and motorcycle are conserved.
Momentum conservation applies to systems, not individual objects, unless they are isolated (which is not the case in a collision). In a collision, the total momentum of the system (in this case, the lorry and the motorcycle together) before the collision is conserved and equals the total momentum of the system after the collision. Individual momentums can change as long as the system’s total momentum remains constant.
4. Total kinetic energy of lorry and motorcycle is conserved.
Kinetic energy is not always conserved in collisions. In elastic collisions, kinetic energy is conserved, but in inelastic collisions, it is not. The conservation of kinetic energy depends on the nature of the collision. To determine if kinetic energy is conserved, we would calculate the total kinetic energy before and after the collision. However, the change in speeds provided suggests a significant interaction that likely resulted in energy being converted to other forms (e.g., sound, heat), indicating that kinetic energy was not conserved.
Given these explanations, the most accurate statement is:
Magnitudes of impulses experienced by lorry and motorcycle during the collision are the same.
This aligns with the principle that in a collision, the impulse (and thus the change in momentum) experienced by each object involved is equal in magnitude and opposite in direction, according to Newton’s third law of motion.
Answer: 2
Example 3
A 5.00 kg object moves at 15.0 ms-1. It collides perfectly inelastically with a 10.0 kg object which was at rest. How much kinetic energy is lost in the collision?
Click here to show/hide answer
Let
- $m_1$ be the 5.00 kg object
- $m_2$ be the 10.00 kg object
- $m_f$ be the 15.0 kg object (result of the collision)
Using conservation of momentum,
$$\begin{aligned} m_1u_1 + m_2u_2 &= m_fv \\ 5.00(15.0) + 10.0(0) &= 15.0(v) \\ v &= 5.00 \, \text{m s}^{-1} \end{aligned}$$
$$\begin{aligned} \text{Loss of kinetic energy} &= \frac{1}{2}m_1u_1^2 – \frac{1}{2}m_fv^2 \\ &= \frac{1}{2}(5.00)(15.0)^2 – \frac{1}{2}(15.0)(5.00)^2 \\ &= 375 \, \text{J} \end{aligned}$$
Answer: 375 J
Example 4: Understanding Conservation of Momentum
In a closed system, two carts on a frictionless track collide head-on. Cart 1 has a mass of 2 kg and is moving at $4\, \text{m/s}$, while Cart 2 has a mass of 3 kg and is moving at $-2\, \text{m/s}$ towards Cart 1. Assuming no external forces act on the system, what is the total momentum of the system before and after the collision?
Click here to show/hide answer
First, calculate the initial momentum of each cart and then the total initial momentum of the system.
- Initial momentum of Cart 1: $p_{1i} = m_1v_{1i} = 2 \times 4 = 8\, \text{kg m/s}$
- Initial momentum of Cart 2: $p_{2i} = m_2v_{2i} = 3 \times (-2) = -6\, \text{kg m/s}$
- Total initial momentum: $p_{\text{total},i} = p_{1i} + p_{2i} = 8-6 = 2\, \text{kg m/s}$
According to the conservation of momentum, the total momentum before the collision equals the total momentum after the collision.
Therefore, the total momentum of the system after the collision remains $2\, \text{kg m/s}$.
Example 5: Predicting Post-Collision Velocities
Using the scenario from Example 4, if the two carts stick together after colliding, what is their combined velocity immediately after the collision?
Click here to show/hide answer
Since the carts stick together, they will have the same final velocity $v_f$. The combined mass of the carts is $2 + 3 = 5\, \text{kg}$, and the total momentum of the system is conserved at $2\, \text{kg m/s}$.
Using the conservation of momentum, $p_{\text{total},i} = p_{\text{total},f}$, and knowing that $p_{\text{total},f} = (m_1 + m_2)v_f$,
$$2 = 5v_f$$
Solving for $v_f$,
$$v_f = \frac{2}{5} = 0.4\, \text{m/s}$$
Thus, the combined velocity of the carts immediately after the collision is $0.4\, \text{m/s}$.