Faraday’s Law of Induction
Faraday’s law of induction states that the induced e.m.f. in a closed loop equals the negative of the time rate of change of magnetic flux through the loop.
$$\epsilon =- \frac{d\Phi_{B}}{dt}$$
Example: E.M.F. and current induced in a loop
The magnetic field between the poles of the electromagnet is uniform at any time, but its magnitude is increasing at the rate of 0.020 T/s. The area of the conducting loop in the field is $120 \, \text{cm}^{2}$, and the total circuit resistance, including the meter and the resistor, is $5.0 \, \Omega$. The induced e.m.f. and the induced current in the circuit is given by:
$$\begin{aligned} \epsilon &= \frac{dB}{dt}A \\ &= 0.24 \, \text{mV} \end{aligned}$$
$$\begin{aligned} I &= \frac{\epsilon}{R} \\ &= 0.048 \, \text{mA} \end{aligned}$$
If we have a coil with N identical turns, and if the flux varies at the same rate through each turn, the total rate of change through all the turns is N times a large as for a single turn. If $\Phi_{B}$ is the flux through each turn, the total e.m.f. in a coil with N turns is:
$$\epsilon =- N \frac{d\Phi_{B}}{dt}$$
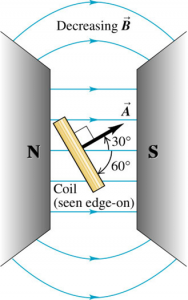
Example: Magnitude & Direction Of An Induced E.M.F.
A coil of wire containing 500 circular loops with radius 4.00 cm is placed between the poles of a large electromagnet, where the magnetic field is uniform and at an angle of $60^{\circ}$ with the place of the coil. The field decreases at a rate of 0.200 T/s. The magnitude of the induced e.m.f.:
$$\begin{aligned} \epsilon &=-500 (-0.2)(0.04^{2} \pi) \cos{30^{\circ}} \\ &= 0.435 \, \text{V} \end{aligned}$$
Lenz’s Law
We can find the direction of an induced e.m.f. or current by using:
$$\epsilon =- \frac{d \Phi_{B}}{dt}$$.
Lenz’s law states that the direction of any magnetic induction effect is such as to oppose the cause of the effect.
Lenz’s law is directy related to energy conservation.
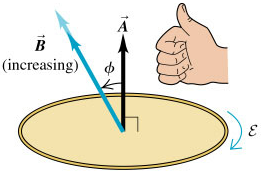
Example 1
Recall that:
$$\begin{aligned} \Phi_{B} &= \vec{B}.\vec{A} \\ &= BA \cos{\phi} > 0 \end{aligned}$$
Since $|\vec{B}|$ is increasing with time,
$$\frac{d\Phi_{B}}{dt} > 0$$
Therefore,
$$\epsilon =-\frac{d \Phi_{B}}{dt} < 0$$
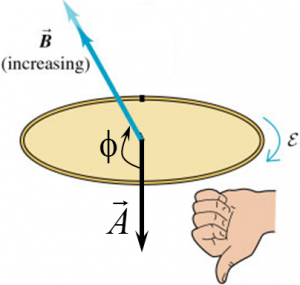
Example 2
$$\begin{aligned} \Phi_{B} &= \vec{B}.\vec{A} \\ &= BA \cos{\phi} < 0 \end{aligned}$$
Since $|\vec{B}|$ is increasing with time,
$$\frac{d\Phi_{B}}{dt} < 0 $$
Therefore,
$$\epsilon =-\frac{d\Phi_{B}}{dt} > 0$$
Next: Examples Involving Faraday’s Law
Previous: Electromagnetic Induction Experiments
Back To Electromagnetism (UY1)