The probability of finding a particle in the speed interval v to v + dv is given by:
$$P (v) = 4 \pi v^{2} \left( \frac{m}{2 \pi k_{B} T} \right)^{\frac{3}{2}} e^{- \frac{m v^{2}}{2 k_{B} T}}$$
, where
- $4 \pi v^{2}$ is the density of states
- $- \frac{m v^{2}}{2 k_{B} T}$ is the ratio of kinetic energy to thermal energy
- $\left( \frac{m}{2 \pi k_{B} T} \right)^{\frac{3}{2}} e^{- \frac{m v^{2}}{2 k_{B} T}}$ is the Boltzmann distribution
a) P(v) = 0 at v = 0 and as v tends to infinity.
b) P(v) reaches a maximum at some intermediate value of v.
– The position of this peak and the shape of the distribution function varies with temperature: As temperature increases, the peak occurs at higher v and the width of the distribution becomes broader: the average speed increases and a larger fraction of molecules can attain very high speeds.
Various measures of the characteristic speed
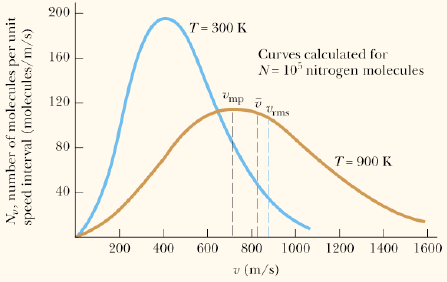 – vmp is the most probable speed at the peak of the distribution function.
– vmp is the most probable speed at the peak of the distribution function.
– vav is the average speed of the distribution.
– Note: vrms > vav > vmp
The most probable speed
The most probable speed occurs at:
$$\frac{d P(v)}{dv} = 0$$
hence,
$$v_{mp} = \sqrt{\frac{2 k_{B} T}{m}}$$
The average speed
The average speed is given by:
$$\bar{v} = \int\limits_{0}^{\infty} P(v) \, v \, dv$$
hence,
$$\bar{v} = \sqrt{\frac{8 k_{B} T}{\pi m}}$$
The root-mean-square speed
The root-mean-square speed is given by:
$$v_{\text{rms}} = \left( \int\limits_{0}^{\infty} P(v) \, v^{2} \, dv \right)^{\frac{1}{2}}$$
hence,
$$v_{\text{rms}} = \sqrt{\frac{3 k_{B} T}{m}}$$
Next: Theorem Of Equipartition Of Energy