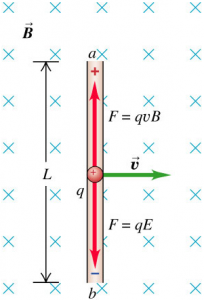
Consider a rod of length L moving through a magnetic field as shown below:
A positively charged particle q in the rod experiences a magnetic force:
$$\vec{F} = q \vec{v} \times \vec{B}$$
Charge will continue to accumulate at the ends of the rod until the electric field $\vec{E}$ within the rod satifies:
$$qE = qvB$$
Hence, the voltage difference of the ends of the rod, $V_{ab}$, is given by:
$$\begin{aligned} V_{ab} &= EL \\ &= vBL \end{aligned}$$
When a conductor moves in a magnetic field, we can understand the induced e.m.f. on the basis of magnetic forces on charges in the conductor.
To generalize the concept of motional e.m.f. for a conductor with any shape, moving in any magnetic field, uniform or not (assuming that the magnetic field at each point does not vary with time), consider an element $d\vec{l}$ of conductor,
$$d\epsilon = (\vec{v} \times \vec{B}) . d\vec{l}$$
For any close conducting loop, the total e.m.f. will be given by:
$$\epsilon = \oint \left( \vec{v} \times \vec{B} \right) . d\vec{l}$$
The above equation is an alternative formulation of Faraday’s law.
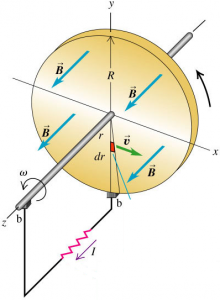
Example: The Faraday Disk Dynamo
Consider a conducting disk with radius R, lying in the xy-plane and rotates with constant angular velocity $\omega$ about z-axis. The disk is in a uniform, constant $\vec{B}$ field parallel to the z-axis. Find the induced e.m.f. between the center and the rim of the disk:
$$\begin{aligned} \epsilon &= \oint \left( \vec{v} \times \vec{B} \right) . d\vec{l} \\ &= \int\limits_{0}^{R} r \omega B \, dr \\ &= \frac{1}{2} \omega B R^{2} \end{aligned}$$