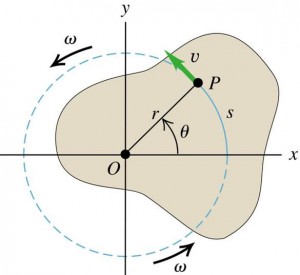
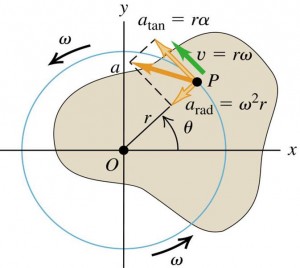
Rotation of an extended object $\rightarrow$ different parts of an object have different linear velocities & accelerations. (However, $\omega$ is constant for the different parts of the rigid object.)
One common assumption to simplify analysis of rotating objects is that the objects are rigid (non-deformable [Object never changes its shape] and internal motion of the object is neglected). However, this assumption is not necessarily true. (E.g. rotating moclecules, galaxies, etc.) Note: Of course, this is just an idealisation of the real world.
Pure rotational motion $\rightarrow$ rotation of a rigid object about a fixed axis.
Since the object is rigid, this means that we can associate the angle $\theta$ with the entire rigid object as well as with an individual particle.
When rotating about a fixed axis, every point on a rigid body has the same angular speed and the same angular acceleration.
Choosing the axis of rotation to be z-axis, we can start to analyse rigid body rotation.
It is more convenient to use polar coordinates as only $\theta$ changes.
Then:
$$\begin{aligned}s \, &=r\theta\\ \theta \, &=\frac{s}{r} \end{aligned}$$
The unit of $\theta$ is radian (rad). One radian is the angle subtended by an arc length equal to the radius of the arc.
Since $360^{\circ} = 2\pi \, \text{rad}$, $1 \, \text{rad} = \frac{360^{\circ}}{2 \pi} = \frac{180^{\circ}}{\pi} \approx 57.30^{\circ}$
Basic Equations For Rigid Body Rotation
Average angular velocity:
$$\bar{\omega} = \frac{\theta_{2}-\theta_{1}}{t_{2}-t_{1}} = \frac{\Delta \theta}{\Delta t}$$
,where $\Delta \theta$ is the angular displacement of the rigid object.
Instantaneous angular velocity:
$$\omega = \lim_{\Delta \rightarrow 0}{\frac{\Delta \theta}{\Delta t}} = \frac{d \theta}{d t}$$
Average angular acceleration:
$$\bar{\alpha} = \frac{\omega_{2}-\omega_{1}}{t_{2}-t_{1}} = \frac{\Delta \omega}{\Delta t}$$
Instantaneous angular acceleration:
$$\alpha = \lim_{\Delta t \rightarrow 0}{\frac{\Delta \omega}{\Delta t}} = \frac{d \omega}{dt}$$
When a rigid body rotates about a fixed axis, every particle in the body moves with the same angular speed $\omega$.
Since $s = r\theta$, we have:
$$\begin{aligned} v \, &= \frac{ds}{dt} \\ &= r \frac{d \theta}{dt} \\ &= r \omega \end{aligned}$$
Using $v = r \omega$, we have:
$$\begin{aligned} a_{t} \, &= \frac{dv}{dt} \\ &= r \frac{d \omega}{dt} \\ &= r \alpha \end{aligned}$$
Where $a_{t}$ is the tangential acceleration of the rigid body.
You will be familiar with the radial acceleration from circular motion:
$$a_{r} = \frac{v^{2}}{r} = r \omega^{2}$$
What we have done above is to link the angular and linear quantities of a rotating rigid body.