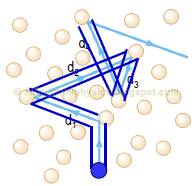
Now, we wish to quantify the particle-particle collisions in this ideal gas. To do this, we need to “switch on” the idea that the particles have size.
Let us define the mean free path, $l$ to be the average distance travelled by the particles between collisions.
$$l = \frac{1}{n} \sum\limits_{i = 1}^{n} d_{i}$$
where
- n is the number of collisions
- $d_{i}$ is the distance between collision
- $\sum\limits_{i = 1}^{n} d_{i}$ will then be the total distance travelled
Finding the mean free path:
Assuming that the particles are identical spheres with diameter d. The particle under discussion (blue) is travelling with an average speed of < v >. It sweeps out a “collision” cylinder in space of diameter 2d which gives collision with other particles if their centres are inside this cylinder. Let us first assume that these other particles (red) are stationary.
Note: “Collision” volume: All stationary particles with centre-of-mass lying inside this cylinder will be hit by the moving blue particle
In time interval t, the “collision” volume is:
$$\begin{aligned} v_{\text{cylinder}} &= \text{area of top of cylinder} \times \text{height of cylinder} \\ &= \pi d^{2} \times \left< v \right> t \end{aligned}$$
Note: If you are wondering about the < v >t, it is just the distance that the blue particle travelled in time t.
The number of collisions during this time t is given by the number of stationary particles in this volume:
$$n = N_{d} \times V_{\text{cylinder}}$$
, where
Nd is the number density of particles
Since the total distance travelled is < v >t, and using the first equation for mean free path:
$$l = \frac{1}{N_{d} \pi d^{2} \left< v \right> t} \left( \left< v \right> t \right)$$
Hence,
$$l = \frac{1}{N_{d} \pi d^{2}}$$
Note: The above equation assumes that only the blue particle is moving, which is obviously not true.
Actually, all the particles are moving with the same $\left< v \right>$. In this case, it is the average relative velocity between the particles that determines the number of collisons. This average relative velocity is given by $\sqrt{2} \bar{v}$.
Hence, the mean free path is:
$$l = \frac{1}{\sqrt{2} \pi N_{d} d^{2}}$$
The average time between collisions is given by:
$$\begin{aligned} t_{\text{coll}} &= \frac{l}{\left< v \right>} \\ &= \frac{1}{\sqrt{2} \pi N_{d} d^{2} \left< v \right>} \end{aligned}$$
The collision frequency is given by:
$$\begin{aligned} f_{\text{coll}} &= \frac{1}{t_{\text{coll}}} \\ &= \sqrt{2} \pi N_{d} d^{2} \left< v \right> \end{aligned}$$
Next: The Boltzmann Distribution