Activity, Half-life and Decay constant

The activity of a radioactive substance is defined as the average number of atoms disintegrating per unit time.

• An activity of one decay per second is one Becquerel (1 Bq)

Activity A is directly proportional to the number of parent nuclei N present at that instant:

$\begin{aligned}A & \propto N \\ A & = \, – \, \frac{dN}{dt} \\ & = \lambda N \end{aligned}$

, where

• N is number of parent nuclei,
• t is the time,
• λ is the decay constant.

The decay constant λ of a nucleus is defined as its probability of decay per unit time.

Half-life is defined as the time taken for half the original number of radioactive nuclei to decay.

Useful Equations:

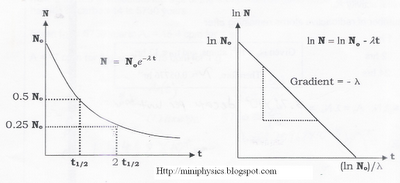
$N = N_{o} \, e^{-\lambda t}$, where

• N_o is the initial number of radioactive nuclides and
• N is the number of nuclides remaining after a time t.

 

$t_{\frac{1}{2}} = \frac{ln \, 2}{\lambda}$, t_1/2 is half-life.

$\left( \frac{N}{N_{o}} \right) = \left( \frac{1}{2} \right)^{n}$ , where n is the number of half-life passed.

 

Graphical Representation of Decay of Parent Nuclide