Kirchhoff’s second law states that the net electromotive force around a closed circuit loop is equal to the sum of potential drops around the loop. OR The algebraic sum of the changes in potential encountered in a complete traversal of a closed circuit loop must be zero.
Kirchhoff’s second law or voltage law is a consequence of the law of conservation of energy.
- If a charge moves around a closed loop in a circuit, it must gain as much energy as it loses.
- Hence, the gain in electrical energy by the charge = corresponding losses in energy through resistances.
Note: You might understand it better after going through the examples. You can find more examples on Kirchhoff’s laws here.
Application of Kirchhoff’s Second Law
- Defining our sign convention, (IMPORTANT!)
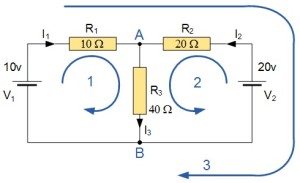
Learning with example
Step 1: Draw closed loops in the circuit.
Step 2: Define the direction of flow of current in the circuit. (As seen in the above diagram) Note that the direction does not have to be the ACTUAL direction in which the current is flowing.
Using Kirchhoff’s First Law,
At A and B,
$$I_{1} + I_{2} = I_{3}$$
Using Kirchhoff’s Second Law and the above sign convention,
Loop 1 yields:
$$\begin{aligned} 10 &= R_{1} \times I_{1} + R_{3} \times I_{3} \\ &= 10I_{1} + 40 I_{3} \\ 1 &= I_{1} + 4 I_{3}\end{aligned}$$
Loop 2 yields:
$$\begin{aligned} 20 &= R_{2} \times I_{2} + R_{3} \times I_{3} \\ &= 20I_{2} + 40 I_{3} \\ 1 &= I_{2} + 2 I_{3} \end{aligned}$$
Loop 3 yields:
$$\begin{aligned} 10 – 20 &= 10 I_{1} – 20 I_{2} \\ 1 &= \, – I_{1} + 2 I_{2} \end{aligned}$$
Using the $I_{1} + I_{2} = I_{3}$ from Kirchhoff’s First Law,
Equation from loop 1 reduces to: (Substitute $I_{3} = I_{1} + I_{2}$ into the equation)
$$1 = 5 I_{1} + 4 I_{2}$$
Equation from loop 2 reduces to: (Substitute $I_{3} = I_{1} + I_{2}$ into the equation)
$$1 = 2 I_{1} + 3 I_{2}$$
This will give:
$$ I_{1} = \, – \frac{1}{3} I_{2}$$
Using the last loop 3 equation,
$$\begin{aligned} 1 &= \frac{1}{3} I_{2} + 2 I_{2} \\ I_{2} &= 0.429 \, A \\ I_{1} &= \, – 0.143 \, A \\ I_{3} &= 0.286 \, A \end{aligned}$$