The second law of thermodynamics is based on experimental observations.
It places constraints on
- the direction of heat flow
- the attainable efficiencies of heat engines and heat pumps, beyond the first law which says only that energy has to be conserved.
2nd Law (Heat engines): The Kelvin-Planck statement
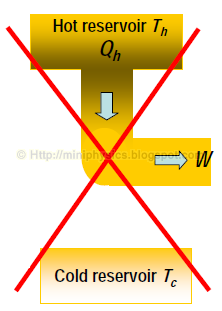 It is impossible to construct a heat engine operating in a cycle, that simply absorbs heat from a reservoir and produces an equal amount of work.
It is impossible to construct a heat engine operating in a cycle, that simply absorbs heat from a reservoir and produces an equal amount of work.
– In other words, it is not possible to have an engine with efficiency e = 100%. The engine cannot operate with Qc = 0
This form of the second law says that heat cannot be entirely converted into mechanical work in a cycle. You cannot make a perfect 100% efficient heat engine!
2nd Law (Heat pumps): The Clausius Statement
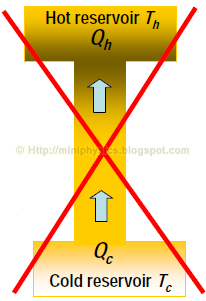 It is impossible to construct a heat pump that provides a continuous transfer of heat from the cold reservoir to the hot reservoir without the input of work.
It is impossible to construct a heat pump that provides a continuous transfer of heat from the cold reservoir to the hot reservoir without the input of work.
– In other words, it is not possible to have a heat pump with infinite Kc or Kh.
This form of the second law says that heat does not flow spontaneously from a cold body to a hot body. You cannot make a perfect heat pump/ refrigerator that does not require input of work.
Equivalence of the Kelvin-Planck and Clausius Statements
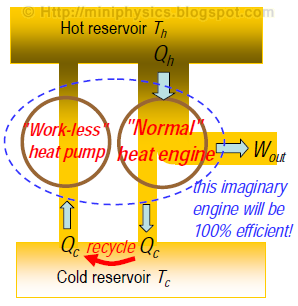 Thought experiment: If we could build a ‘work-less’ heat pump that violates Clausius form of the second law, we could in principle join it with a “normal” heat engine to recycle the rejected heat, and therefore make a combination that ultimately converts all heat into work.
Thought experiment: If we could build a ‘work-less’ heat pump that violates Clausius form of the second law, we could in principle join it with a “normal” heat engine to recycle the rejected heat, and therefore make a combination that ultimately converts all heat into work.
The operation of this combination engine will therefore violate the Kelvin-Planck form of the second law.
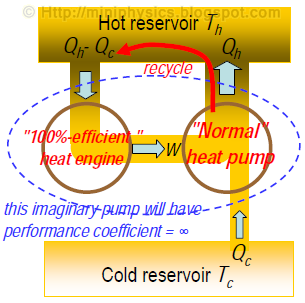 Conversely, if we could build a 100% efficient heat engine that violates the Kelvin-Planck form of the second law, and converts all heat input from the hot reservoir into work, then we could in principle join it with a “normal” heat pump to keep pumping heat continuously from the cold to the hot reservoir without requiring continuous work input.
Conversely, if we could build a 100% efficient heat engine that violates the Kelvin-Planck form of the second law, and converts all heat input from the hot reservoir into work, then we could in principle join it with a “normal” heat pump to keep pumping heat continuously from the cold to the hot reservoir without requiring continuous work input.
This violates the Clausius form of the second law.
Therefore if either the Kelvin-Planck or the Clausius statements are untrue, the other will also be untrue. Hence, if Kelvin-Planck statement is true, the Clausius statement is also true. Both statements are thus equivalent.