Now, what is the maximum fraction of the heat input that can be converted into work using cyclical processes?
In 1824, a French engineer named Sadi Carnot described a theoretical engine, now called a Carnot engine, that is of great importance from both practical and theoretical viewpoints. He showed that a heat engine operating in an ideal, reversible cycle – called a Carnot cycle – between two energy reservoirs is the most efficient engine possible. Such an ideal engine establishes an upper limit on the efficiencies of all real engines. that is, the net work done by a working substance taken through the Carnot cycle is the greatest amount of work possible for a given amount of energy supplied to the substance at the upper temperature.
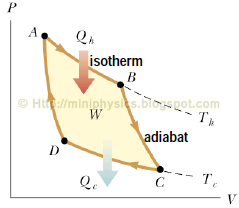 The Carnot cycle comprises of four reversible processes operating between a hot reservoir Th and a cold reservoir Tc:
The Carnot cycle comprises of four reversible processes operating between a hot reservoir Th and a cold reservoir Tc:
(a) an isothermal expansion (A to B) at Th in which the gas is placed in thermal contact with an energy reservoir at temperature Th. During the process, the gas absorbs energy Qh by heat from the reservoir and does work WAB in raising the piston.
(b) an adiabatic expansion (B to C), the base of the cylinder is replaced by a thermally non-conducting wall and the gas expands adiabatically; that is; no energy enters or leaves the system by heat. During the process, the temperature falls from Th to Tc and the gas does work WBC in raising the piston.
(c) an isothermal compression (C to D) at Tc. The gas is placed in thermal contact with an energy reservoir at temperature Tc and is compressed isothermally at temperature Tc. During this time, the gas expels energy Qc to the reservoir and the work done on the gas is WCD.
(d) an adiabatic compression (D to A) that takes it back to the starting state. The base of the cylinder is again replaced by a thermally non-conducting wall and the gas is compressed adiabatically. The temperature of the gas increases to Th, and the work done on the gas is WDA.
The thermal efficiency of a Carnot engine is:
$$e_{c} = 1 – \frac{T_{c}}{T_{h}}$$
No engine cycle operating between a hot and a cold reservoir can be more efficient than the Carnot cycle operating between the two reservoirs.
This means:
$$e \le 1 \, – \frac{T_{c}}{T_{h}}$$
Note: A Carnot engine cycle takes in heat isothermally from the hot reservoir and rejects waste heat isothermally into the cold reservoir. Other engine cycles may not do the heat transfers isothermally.
In other words, for a given set of hot and cold reservoirs, the Carnot engine cycle is the one that makes use of the heat input most efficiently.
Note that this theorem does not depend on the actual processes or mechanical details of other engines, only on the temperatures of the hot and cold reservoirs between which they operate.
Practicality
The Carnot cycle unfortunately is not a practical engine cycle because it requires reversible isothermal processes which can transfer heat into the engine only very slowly, and so they are not of practical value. The reversible adiabatic processes on the other hand are quite easy to implement practically.
As D. Schroeder in An Introduction to Thermal Physics puts it “So don’t bother installing a Carnot engine in your car, while it would increase your (petrol) mileage, you would be passed on the (expressway) by pedestrians.)
Hint: You can derive the thermal efficiency of a Carnot engine by considering the adiabatic relationship of the two temperatures.
Why is the Carnot cycle the most efficient?
Thought experiment: Why no cycle can be more efficient than the Carnot cycle.
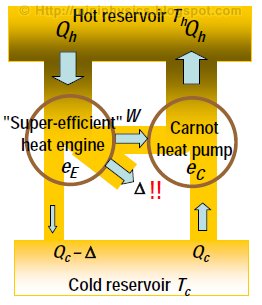 Imagine operating the Carnot engine in reverse as a heat pump. This pump has $e_{\text{carnot}} = \frac{W_{\text{in}}}{Q_{h}}$ because the Carnot cycle is reversible.
Imagine operating the Carnot engine in reverse as a heat pump. This pump has $e_{\text{carnot}} = \frac{W_{\text{in}}}{Q_{h}}$ because the Carnot cycle is reversible.
Imagine now, we join a heat engine E to this Carnot heat pump, and make this heat engine E extract some amount of heat from the hot reservoir as the Carnot pump is discharging into that reservoir.
If the engine cycle E were more efficient than the Carnot engine cycle, then it can produce more work than what went into the Carnot pump, and thus achieve a perfect conversion of heat into work. This situation violates the 2nd law and is therefore impossible.
Thus eE ≤ eC for all engine cycles operating between a given Tc and Th.