UY1: Heat Engines – Thermal Efficiency

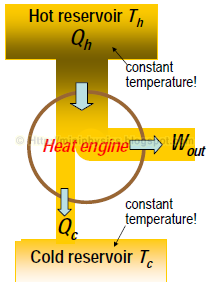
First law for an engine cycle says:

W_out = Q_h – Q_c

,where
W_out is work output by engine
Q_h is heat input from hot reservoir
Q_c is heat output to cold reservoir

Thermal efficiency is defined to be the ratio of work output to the heat input from the hot reservoir per cycle,

$$\begin{aligned} e \, &= \frac{W_{\text{out}}}{Q_{h}} \\ &= \frac{Q_{h} \, – Q_{c}}{Q_{h}} \\ &= 1 \, – \frac{Q_{c}}{Q_{h}} \end{aligned}$$

This thermal efficiency is simply 1 minus the fraction of heat rejected into the cold reservoir.

 

Heat Pump: Coefficients of performance

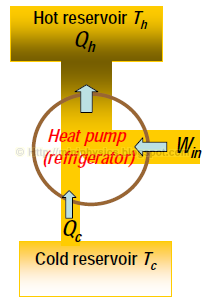
First law for a heat pump is:

$$W_{\text{in}} = Q_{h} – Q_{c}$$

Here, Q_h is defined as heat output to hot reservoir and Q_c is heat input from cold reservoir, because we are dealing with a heat pump.

In the heating mode, where we are interested in the ratio of heat output into the hot reservoir to the work input per cycle, we define coefficient of performance (for heating):

$$K_{h} = \frac{Q_{h}}{W_{\text{in}}} = \frac{Q_{h}}{Q_{h} – Q_{c}}$$

In the cooling mode, where we are interested in the ratio of heat extracted from the cold reservoir to the work input per cycle, we define coefficient of performance (for cooling):

$$K_{c} = \frac{Q_{c}}{W_{\text{in}}} = \frac{Q_{c}}{Q_{h} – Q_{c}}$$

 

Next: Definition of second law of thermodynamics

Previous: Heat pumps

Back To Thermodynamics