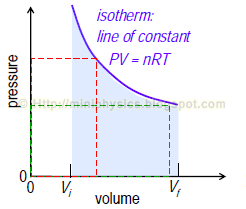
In an isothermal process, the temperature of the system is unchanged. (ΔT = 0). For this process, the first law gives ΔE = 0, thus Q = -W.
This means that the net heat input into the system equals to the net work output by the system.
From the ideal gas equation, P1V1 = P2V2 = nRT (isotherm).
Isothermal work done by the gas,
$$\begin{aligned} W_{\text{out}} &= \int\limits_{V_{i}}^{V_{f}} P \, dV \\ &= \int\limits_{V_{i}}^{V_{f}} \frac{nRT}{V} \, dV \\ &= nRT \, \text{ln} \, \frac{V_{f}}{V_{i}} \end{aligned}$$
Note: Since PV = constant, the area of red rectangle = green rectangle. This geometric property will be useful to solve heat cycle problems.