In engines, a gas is often employed to perform work through gas expansion or pressure-volume work.
Infinitesimal work output by the gas for an infinitesimal piston displacement dy is given by:
$$\begin{aligned} dW_{\text{out}} &= F \, dy \\ &= PA \, dy \\ &= P \, dV \end{aligned}$$
, where
F is the force exerted by the gas on the piston
y is the outward piston displacement
P is gas pressure
A is piston area
V is gas volume
Conversely, infinitesimal work input to the gas is given by: dWin = -dWout
The work output for a finite volume change from Vi Vf is:
$$\begin{aligned} W_{\text{out}} &= \int\limits_{1}^{2} dW_{out} \\ &= \int\limits_{V_{1}}^{V_{2}} P \, dV \end{aligned}$$
Geometrically, this is simply the area under the PV curve that represents the piston process, integrated from start volume V1 to end volume V2
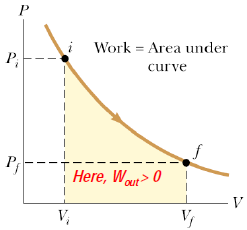
If piston opens, i.e., V2 > V1, Wout > 0.
If piston closes, i.e., V2 < V1, Wout < 0.