In classical mechanics, we are concerned with the concepts of work and energy.
Work-energy concepts are based on Newton’s laws and do not involve any new physical principles.
The work-energy concept can therefore be applied to the dynamics of a mechanical system without resorting to Newton’s laws. This is useful in complex situation (e.g. variable forces) and applicable to a wide range of phenomena.
Energy
Energy is present in the Universe in various forms.
Energy can be transformed from one form to another.
Conservation of energy states that when energy is changed from one form to another, the total amount in the system remains the same.
Work Done By A Constant Force
When force is parallel to displacement, Work done by a force = force $\times$ displacement
$$W = Fs$$
The SI unit is $\text{N m}$ or joule $\left( J \right)$.
In general, the work done by an agent exerting a constant force is the product of the component of the force in the direction of the displacement and the magnitude of the displacement of the force.
When the force is an an angle $\phi$ to the displacement,
$$\begin{aligned} W &= Fs \cos{\phi} \\ W &= \vec{F}.\vec{s} \end{aligned}$$
A force does no work if the object does not move.
Work done by a force is zero if the force is perpendicular to the displacement.
Work can be positive or negative. E.g. When an object is lifted from the ground, the work done by the applied force is positive, while the work done by the gravitational force is negative.
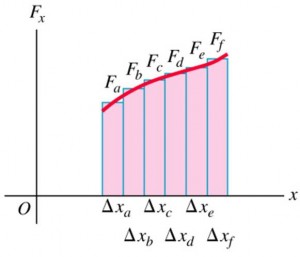
Work Done By A Varying Force
For a varying force $\vec{F} \left( x \right)$, consider the work done over a small displacement $\Delta \vec{x}_{i}$.
$$\Delta W = F_{i} \Delta x_{i}$$
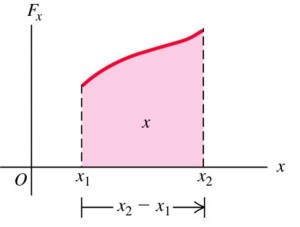
Total work done from the displacement from $x_{1}$ to $x_{2}$ is:
$$W \approx \sum F_{i} \Delta x_{i}$$
In the limit that $\Delta x \rightarrow 0$, we have:
$$W = \int\limits_{x_{1}}^{x_{2}} F_{x} \, dx$$
The work done by the component $F_{x}$ of the varying force as the particle moves from $x_{1}$ to $x_{2}$ is equal to the area under the curve.
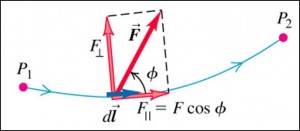
Work along a curved path
In general, for a varying force along a curved path, small element of work done $dW$ during displacement $d\vec{l}$ is:
$$\begin{aligned} dW &= \vec{F} \cos{\theta} \, dl \\ &= F_{||} \, dl \\ &= \vec{F}.d\vec{l} \end{aligned}$$
Total work done along path $P_{1}$ to $P_{2}$ is:
$$\begin{aligned} W &= \int\limits_{P_{1}}^{P_{2}} F \cos{\theta} \, dl \\ &= \int\limits_{P_{1}}^{P_{2}} F_{||} \, dl \\ &= \int\limits_{P_{1}}^{P_{2}} \vec{F} . d \vec{l} \end{aligned}$$
Note that the component of force perpendicular to path, $F_{\perp} = F \sin{\theta}$, does no work.
Previous: Uniform Circular Motion & Non-uniform Circular Motion