Uniform Circular Motion
A particle moving with uniform speed $v$ in a circular path of radius $r$ experiences an acceleration $\vec{a}_{r}$ that has a magnitude:
$$a_{r} = \frac{v^{2}}{r}$$
$\vec{a}_{r}$ is directed towards the center of the circle (centripetal acceleration)
$\vec{a}_{r}$ is always perpendicular to $\vec{v}$
Applying Newton’s Second Law along the radial direction:
$$\sum F_{r} = ma_{r} = m\frac{v^{2}}{r}$$
A force causing centripetal acceleration acts towards the centre of the circular path and causes a change in the direction of the velocity vector (central force).
Non-uniform Circular Motion
In this case, the acceleration is comprised of radial acceleration and tangential acceleration.
$$\vec{a} = \vec{a}_{r} + \vec{a}_{t}$$
Hence, the forces involved:
$$\vec{F} = \vec{F}_{r} + \vec{F}_{t}$$
$\vec{F}_{r}$ is directed towards the centre of the circle and is responsible for the centripetal acceleration. $\vec{F}_{t}$ is tangential to the circle and is responsible for the tangential acceleration (change in speed).
Example: Mass round a vertical circle
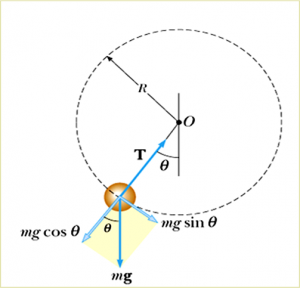
A small sphere of mass $m$ is attached to the end of a cord of length $R$ and whirls in a vertical circle about a fixed point $O$. Determine the tension in the cord at any instant when the speed of the sphere is $v$ and the cord makes an angle $\theta$ with the vertical.
First, we have to resolve the forces into tangential and radial components:
$$\begin{aligned} \sum F_{t} &= mg \sin{\theta} \\ &= ma_{t} \end{aligned}$$
$$\begin{aligned} \sum F_{r} &= T-mg \cos{\theta} \\ &= \frac{mv^{2}}{R} \end{aligned}$$
The tension is given by:
$$T = m \left( \frac{v^{2}}{R} + g \cos{\theta} \right)$$
At the top, where $\theta = 180^{\circ}$,
$$T_{\text{top}} = m \left( \frac{v_{\text{top}}^{2}}{R}-g \right)$$
At the bottom, where $\theta = 0^{\circ}$,
$$T_{\text{bot}} = m \left( \frac{v_{\text{bot}}^{2}}{R} + g \right)$$
Fictitious Forces In Non-inertial Frames
Newton’s laws of motion are only valid when observations are made in an inertial frame of reference.
Fictitious forces must be introduced to make Newton’s laws work in non-inertial (accelerated) frames. One common example is the centrifugal force.
Fictitious forces in a non-inertial frame do not represent real forces on the body as they do not exist when observed from an inertial frame.
Normally, inertial reference frames should be used. But there are cases in which accelerating frames are more convenient.
Case 1: Linear Motion
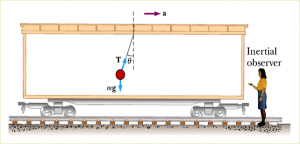
Consider an object having an acceleration of $\vec{a}$. There is a pendulum bob of mass $m$ hanging from the ceiling of the object. Let’s analyze the forces in inertial and non-inertial frames.
In an inertial frame,
$$\sum F_{x} = T \sin{\theta} = ma$$
$$\sum F_{y} = T \cos{\theta}-mg = 0$$
The acceleration is $a = g \tan{\theta}$.
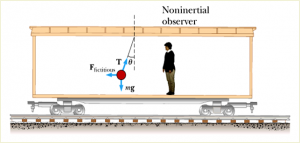
In a non-inertial frame,
$$\sum F_{x}^{\prime} = T \sin{\theta}-F_{\text{fictitious}} = 0$$
$$\sum F_{y}^{\prime} = T \cos{\theta}-mg = 0$$
For the observer in the non-inertial frame, he/she will have to introduce a fictitious force with magnitude $F_{\text{fictitious}} = ma$ to explain the swing in the pendulum pob.
Case 2: Rotating System
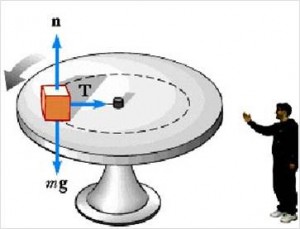
Consider a block undergoing circular motion with the help of a string. Let’s analyze the forces in inertial and non-inertial frames.
In the inertial frame:
If the block rotates uniformly, it undergoes an acceleration of magnitude $\frac{\vec{v}^{2}}{\vec{r}}$. The inertial observer concludes that this centripetal acceleration is provided by the force $\vec{T}$ exerted by the string.
$$T = \frac{mv^{2}}{r}$$
In the non-inertial frame: (one that is rotating with the block)
To the observer, the block is at rest and its acceleration is zero. Therefore, the non-inertial observer must introduce a fictitious outward force of magnitude $\frac{mv^{2}}{r}$ to balance the inward force exerted by the string.
$$F_{\text{fictitious}} = \frac{mv^{2}}{r}$$