Interaction between moving object and medium (liquid, gas) sometimes cannot be neglected.
The medium exerts a resistive force $f$ on the object opposite to its direction of motion. (Common example: Air resistance)
The magnitude of the resistive force, $f$, generally increases with increasing speed. The actual dependence of the magnitude of the resistive force with the speed is complicated. Hence, the common approximations used are as follows:
- For small objects at low speeds. (E.g. Dust in air) $$f = kv$$
- For large objects at high speeds (E.g. Skydiver) $$f = D v^{2}$$
Resistive Forces At Low Speed
Neglecting upthrust or buoyancy force, the vertical forces on the object is:
$$\begin{aligned} \sum F_{y} &= ma \\ &= m \frac{dv}{dt} \end{aligned}$$
Since $f = kv$,
$$\begin{aligned} mg-kv &= m \frac{dv}{dt} \\ \frac{dv}{dt} &= g-\frac{k}{m} v \end{aligned}$$
, where k is a constant. The value of k depends on the medium and the object.
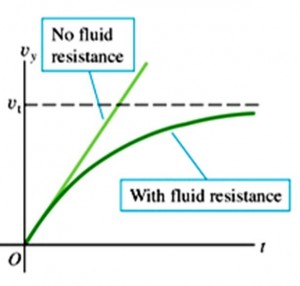
When $v = 0$, the resistive force $-kv$ is also zero and the acceleration is simply $g$.
As t increases, the resistive force increases and the acceleration decreases.
Eventually, the acceleration becomes zero and object moves with a constant speed $v_{t}$, which is the terminal speed. The terminal speed is:
$$\begin{aligned} mg-kv_{t} &= 0 \\ v_{t} &= \frac{mg}{k} \end{aligned}$$
Let’s find v as a function of t, solving $\frac{dv}{dt} = g-\frac{k}{m} v$, we have:
$$v = \frac{mg}{k} \left( 1-e^{-\frac{kt}{m}} \right)$$
Defining the time constant, $\tau = \frac{m}{k}$, we have:
$$v = v_{t} \left( 1-e^{\frac{-t}{\tau}} \right)$$
A graph showing the effect of resistive force on the speed of the object:
Air Drag At High Speeds
For objects moving at high speeds through the air, the resistive force is proportional to the square of the speed,
$$f = Dv^{2}$$
A more detailed formula is:
$$f = \frac{1}{2} D \rho A v^{2}$$
, where
- $\rho$ is the density of air
- $A$ is the cross-sectional area of the falling object; measured in a plane perpendicular to its motion
- $D$ is the drag coefficient
Let’s find the terminal velocity for the more detailed formula. We have:
$$\begin{aligned} mg-\frac{1}{2} D \rho A v^{2} &= ma \\ a &= g-\left( \frac{D \rho A}{2m} \right) v^{2} \\ v_{t} &= \sqrt{\frac{2mg}{D \rho A}} \end{aligned}$$