Consider a parallel plate capacitor. When a dielectric material is inserted between the plates while the charge is kept constant, the potential difference between the plates is reduced by a factor K, where K is the dielectric constant.
$$K \equiv \frac{C}{C_{0}}$$
where $C_{0}$ is the original capacitance of the capacitor and $C$ is the capacitance of the capacitor with the dielectric.
The voltage will also be changed accordingly:
$$V = \frac{V_{0}}{K}$$
Note that the energy stored in the capacitor will change as well. We can see this from:
$$U_{0} = \frac{1}{2} Q V_{0}$$
$$\begin{aligned} U &= \frac{1}{2} QV \\ &= \frac{1}{k} \times \frac{1}{2} Q V_{0} \\ &= \frac{1}{k} \times U_{0} \end{aligned}$$
Reason for the decrease in energy stored: When the dielectric is placed into the capacitor, due to the formation of positive and negative charges, there will be a force by the electric field on the dielectric. A force will be required to prevent the dielectric from accelerating. Energy is taken out of the electric field. Hence, the electric potential energy stored in the electric field decreases.
Normally, dielectric constant is more than 1. Hence, the capacitance of a capacitor of given dimensions is greater when there is a dielectric material between the plates than when there is a vacuum.
The electric field between the plates must also decrease by the same factor:
$$E_{0} = \frac{\sigma}{\epsilon_{0}}$$
$$E = \frac{E_{0}}{K}$$
The electric field can be expressed in terms of the induced charges on the dielectric as well:
$$E = \frac{\sigma – \sigma_{i}}{\epsilon_{0}}$$
To obtain an expression for the induced surface charge density on the dielectric:
$$\begin{aligned} E &= \frac{E_{0}}{K} \\ KE &= E_{0} \\ K \left( \frac{\sigma-\sigma_{i}}{\epsilon_{0}} \right) &= \frac{\sigma}{\epsilon_{0}} \\ \sigma_{i} &= \left( 1 – \frac{1}{K} \right) \sigma \end{aligned}$$
You can calculate the permitivity of the dielectric, $\epsilon$:
$$\begin{aligned} E &= \frac{E_{0}}{K} \\ \frac{\sigma}{\epsilon} &= \frac{\sigma}{\epsilon_{0} K} \\ \epsilon &= \epsilon_{0} K \end{aligned}$$
You can express the electric field, capacitance and energy density using the permitivity of the dielectric:
$$\begin{aligned} E &= \frac{\sigma}{\epsilon} \\ C &= \epsilon \frac{A}{d} \\ u &= \frac{1}{2} \epsilon E^{2} \end{aligned}$$
Dielectric breakdown
When any dielectric material is subjected to a sufficiently strong electric field, dielectric breakdown takes place and the dielectric becomes a conductor.
The maximum electric field magnitude that a material can withstand without the occurence of breakdown is called its dielectric strength which governs the maximum voltage ratings of capacitors.
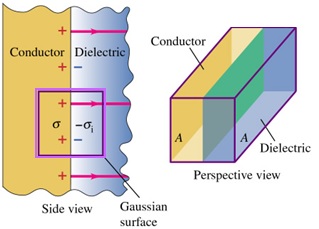
Gauss’s Law In Dielectric
Consider the left capacitor plate and left surface of the dielectric.
$$\begin{aligned} EA &= \frac{(\sigma-\sigma_{i}) A}{\epsilon_{0}} \\ EA &= \frac{\sigma A}{K \epsilon_{0}} \end{aligned}$$
Note that $\sigma_{i} = \left( 1-\frac{1}{K} \right) \sigma$.
In general, for any Gaussian surface, whenever the induced charge in proportional to the electric field in the material,
$$\oint K \vec{E} . d \vec{A} = \frac{Q_{encl-free}}{\epsilon_{0}} $$
where $Q_{encl-free}$ is the total free charge enclosed by the Gaussian surface.
Next: Current, Drift Velocity And Current Density