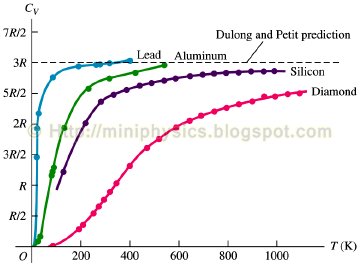
The molar specific heats of solids are often strongly temperature dependent.
Generally, they decrease in a non-linear manner with decreasing temperature and approach zero as the temperature approaches absolute zero. This is explained by quantum theory as the result of more and more vibrational modes becoming “frozen in” and can no longer absorb energy.
At sufficiently high temperatures, the molar heat capacities of mono-atomic solid approach the classical Dulong-Petit law of 3R = 24.9 J K-1 mol-1. For a collection of N atoms, there are 3N – 6 ≈ 3N (for very large N) vibrational modes. Each vibrational mode contributes kBT to the internal energy. Each mole of atoms is therefore expected to contribute 3R to the specific heat by the energy equipartition theorem.
The difference between the molar specific heat at constant volume and that at the constant pressure is small. (Cv ≈ Cp) This is because the solids cannot do significant expansion work. (Unlike a gas)
Temperature dependence of Cv of mono-atomic solids
Next: Definition and concepts of thermodynamics