Question:
Glass is smoother than ice. Yet, why is it you can skate on ice and not on glass?
Answer:
Ice melts under pressure. So, when the steel blades of the skates pressed on the ice, the ice melts. The water formed makes the skates slide easily over the ice, reducing friction. So, when you are skating, you’re skating on a thin film of water, which acts like lubricating oil.
NOTE: The above explanation of ice melting under the pressure is not true! Under the pressure of the skates, the melting point is only increased by ~1 – 3 degrees Celsius, which is not enough to explain the above observation. Currently, as far as I know, research are still going on as to why a low-friction surface develops.
Attempt at a new answer:
It is a common idea among people that skaters slide more easily on ice than other smooth surfaces because ice melts under the pressure exerted by the skates to produce a thin film of water. However, it is DEFINITELY true that an increase in pressure will result in the ice melting.
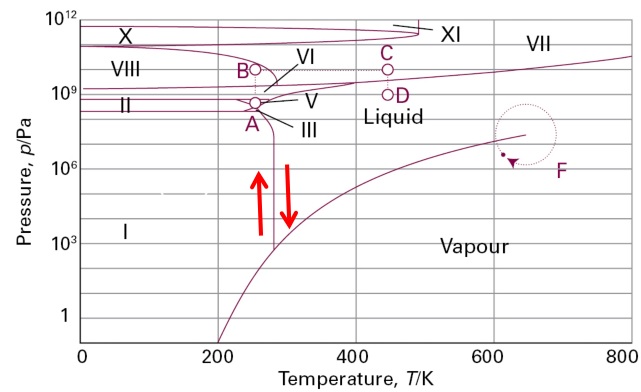
Why increase in pressure will result in the melting of ice?
The picture above shows the phase diagram for water. The roman numerals (I, II, III, ..) are the different phases of ice. You do not need to be distracted by those and just focus on the red arrows at the boundary between liquid and ice I. The boundary has a negative slope (sloping down like $y=-x$ graph). This means that, at a particular temperature (along the temperature range of the boundary), the lower pressure area will correspond to ice I while the higher pressure area will correspond to water. That is equivalent to saying that the melting point of water is lower when a higher pressure is applied to water.
The negative slope of the boundary is linked to the fact that the change in volume is positive as water changes into ice. One can calculate the theoretical required change in pressure for 1 $^{\circ}$C by using the Clapeyron equation.
For a normal adult with a body mass of 75 kg and wearing a pair of skates with blades of dimensions of 30 cm by 3 mm, the pressure is around 400 kPa. From the calculations using the Clapeyron equation, this would translate to a decrease in the melting point of ice of only 0.02 $^{\circ}$C.
From the calculations done by academics, an adult with a body mass of 75 kg would give rise to a decrease in the melting point of ice of only 0.02 $^{\circ}$C (with both feet on ice) or 0.05 $^{\circ}$C (with single foot on ice). This decrease is much too small to cause the formation of liquid film on ice during a typical skating activity. This is due to the fact that skating is normally performed in an environment that is at least a few degrees below 0 $^{\circ}$C. Hence, water should still remain solid at this temperature even when the melting point is lowered to -0.05 $^{\circ}$C due to the exerted pressure.
There must be other reasons that contribute to the slipperiness of ice, such as the fact that ice has a hard and smooth surface, frictional heating and the unique properties of the water molecules on the surface of ice.
The dynamics of ice surfaces has grown into an active research topic today, and more recent studies suggested that the slipperiness of ice (even below its melting point) has a lot to do with the structure at the ice-air interface. Molecular interactions and motions on the interface are different from those in the bulk of ice.