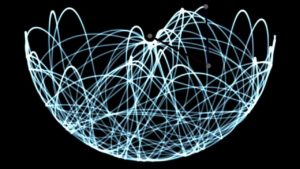
In the tranquil swaying of a grandfather clock or the methodical oscillations of a playground swing, the pendulum finds its place as an emblem of predictability and rhythmic precision. It stands as a testament to the ordered world of classical mechanics, where every motion submits to the calculable laws of physics. However, introduce a twist to this tale by adding another pendulum to the equation, and you venture into a domain where predictability crumbles before your eyes. Welcome to the captivating and erratic world of the double pendulum.
Breaking Down the Basics
Before we dive into the chaos, let’s revisit our protagonist in its simplest form: the single pendulum. Picture it as a weight, or bob, suspended from a fixed point by a rod or string that allows it to swing back and forth under the influence of gravity. The beauty of this system lies in its predictability. Given the length of the string and the angle from which it’s released, physicists can calculate with remarkable accuracy the trajectory, period, and velocity of the pendulum’s swing. This predictability arises from it being a simple harmonic oscillator when its swings are small.
The Leap into Chaos
Now, imagine attaching a second pendulum to the bottom of the first one’s bob, effectively creating a double pendulum. This act transforms our predictable system into one teeming with complexity and unpredictability. At first glance, it might seem like just an extension of the single pendendum scenario—twice as complex but surely manageable? Not quite. The introduction of the second pendulum turns our system into a classic example of chaotic behavior.
Why Does Chaos Ensue?
The chaos emanates from the system’s sensitivity to initial conditions—a hallmark characteristic of chaos theory. In simple terms, even microscopic differences in how you start both pendulums (like a minuscule variation in angle or speed) can lead to dramatically divergent outcomes. This is often encapsulated in the popular metaphor known as the butterfly effect: the flapping of a butterfly’s wings in Brazil could theoretically trigger a tornado in Texas.
In the double pendulum’s case, this sensitivity means predicting its movement over a long period becomes practically impossible. The second pendulum introduces more degrees of freedom, exponentially complicating the dynamics. The upper pendulum influences the motion of the lower one and vice versa, creating an intricate dance of energy transfer and momentum that defies easy prediction.
The Beauty of Chaos
Despite its unpredictability, or perhaps because of it, the double pendulum mesmerizes observers. It serves as a physical demonstration that not all systems are predictable, even in physics, which is often perceived as the most deterministic of sciences. Watching a double pendulum move can be hypnotizing; it lurches from methodical swings into wild gyrations without obvious cause, illustrating chaos in motion.
Understanding Through Simulation
Given its chaotic nature, one might assume studying the double pendulum would be a futile endeavor. Yet, with modern computational tools and sophisticated mathematical techniques, physicists can explore this chaotic system in unprecedented detail. Computer simulations allow us to visualize the double pendulum’s trajectory under various initial conditions, revealing patterns within the chaos.
These simulations not only provide insight into double pendulums but also help scientists understand other chaotic systems encountered in nature, from weather patterns and turbulent fluids to population dynamics and even financial markets.
The Real-World Implications
At first glance, the double pendulum might appear as nothing more than an interesting curiosity—a physicist’s toy demonstrating chaos theory. However, its study offers real-world applications and insights. For instance, understanding chaotic systems helps meteorologists make better predictions about weather and climate change. In engineering, insights from studying chaotic systems like the double pendulum can improve designs for structures that must withstand random forces, such as skyscrapers facing turbulent winds or bridges enduring variable loads.
Embracing Uncertainty
The double pendulum teaches us an invaluable lesson about nature: not everything is predictable—and that’s okay. It reflects a universe that is far richer and more interesting than one governed entirely by linear predictability. In exploring systems like these, scientists embrace uncertainty and develop new mathematical tools and models to probe the boundaries between order and chaos.
This venture into chaos does not undermine scientific endeavor; rather, it enriches it. Understanding chaotic systems provides a clearer picture of our complex world and equips us with better tools for prediction and control where they are possible—and humility where they are not.
Conclusion
The double pendulum stands as a gateway between order and chaos, simplicity and complexity. Its erratic movements challenge our assumptions about predictability in physical systems and offer profound insights into the nature of chaos itself. Far from being merely academic curiosities, studies of such chaotic systems have practical implications across various fields—from meteorology to engineering and beyond.
As we continue to unravel the mysteries of chaotic systems like the double pendulum, we edge closer to understanding—and perhaps appreciating—the inherent unpredictability that threads through our universe.