Resonance In A.C. Circuits
Suppose we connect an A.C. source with constant voltage amplitude V but adjustable angular frequency $\omega$ across an L-R-C series circuit.
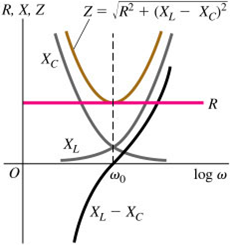
The current that appears in the circuit has the same angular frequency $\omega$ as the source and a current amplitude $I = \frac{V}{Z}$, where the impedance of the L-R-C series circuit is $Z = \sqrt{R^{2} + \left( \omega L-\frac{1}{\omega C} \right)^{2}}$. At the resonance angular frequency, $\omega_{0}$,
$$\begin{aligned} \omega_{0} L-\frac{1}{\omega_{0}C} &= 0 \\ \omega_{0} &= \sqrt{\frac{1}{LC}} \end{aligned}$$
, the impedance has its smallest value: $Z = R$.
When we vary the angular frequency $\omega$ of the source, the current amplitude I will vary as well. The maximum value of I occurs at the resonance angular frequency at which the impedance $Z$ is minimum.
Power In A.C. Circuits
In any A.C. circuit, with any combination of resistors, inductors and capacitors, the voltage v across the entire circuit has some phase angle $\phi$ with respect to the current $i$.
The instantaneous power:
$$\begin{aligned} p &= iv \\ &= I \cos{\omega t} \times V \cos{\omega t + \phi} \\ &= IV \cos{\omega t} \left( \cos{\omega t} \cos{\phi}-\sin{\omega t} \sin{\phi} \right) \\ &= IV \cos{\phi} \cos^{2}{\omega t}-IV \sin{\phi} \cos{\omega t} \sin{\omega t} \\ &= \frac{1}{2} IV \cos{\phi} \left( 1 + \cos{2 \omega t} \right)-\frac{1}{2} IV \sin{\phi} \sin{2 \omega t} \end{aligned}$$
The average power is:
$$\begin{aligned} P_{av} &= \frac{1}{2} IV \cos{\phi} \\ &= I_{\text{rms}} V_{\text{rms}} \cos{\phi} \end{aligned}$$
, where $\cos{\phi}$ is the power factor.
Next: Electromagnetic Spectrum & Sinusoidal EM Plane Waves