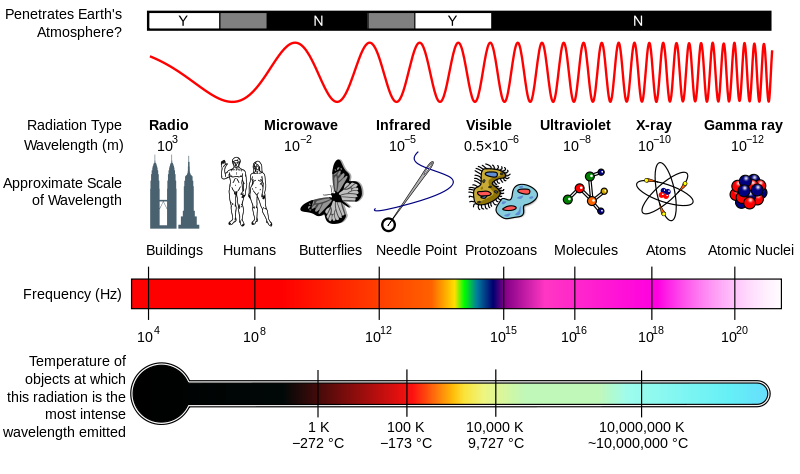
Every accelerated charge radiates electromagnetic energy – electromagnetic waves. Electric and magnetic disturbances radiate away from the source. Electromagnetic waves require no medium. (What’s “waving” in an electromagnetic wave are the time-varying electric and magnetic fields.
The wave travels in vacuum with a definite and unchanging speed $c$ – the speed of light.
Hertz produced pulses of electromagnetic radiation by generating a spark between two conductors. The electromagnetic radiation would travel out in all direction and induce a spark between two metal knobs used to detect the electromagnetic radiation.
The wave is transverse – both $\vec{E}$ and $\vec{B}$ are perpendicular to the direction of propagation of the wave.
- $\vec{E}$ and $\vec{B}$ are mutually perpendicular to each other.
- The direction of propagation is the direction of $\vec{E} \times \vec{B}$.
- There is a definite ratio between the magnitudes of $\vec{E}$ and $\vec{B}$: $E = cB$
Electromagnetic waves have the property of polarization. A wave in which $\vec{E}$ is always parallel to a certain axis is linearly polarized along that axis.
Sinusoidal Electromagnetic Plane Waves
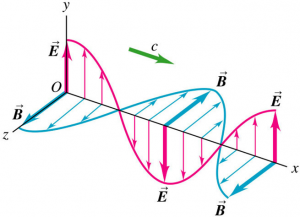
The figure above shows a linearly polarizaed sinusoidal electromagnetic wave travelling in the positive x-direction.
$$\begin{aligned} \vec{E}\left(x,t \right) = E_{\text{max}} \cos{\left( kx-\omega t \right)}\hat{j} \\ \vec{B}\left(x,t \right) = B_{\text{max}} \cos{\left( kx-\omega t \right)}\hat{k} \end{aligned}$$
, where k is the wavenumber: $k = \frac{2 \pi}{\lambda}$ and $\omega$ is the angular frequency: $\omega = 2 \pi f$.
The electric and magnetic fields oscillate in phase. At all points, the vector product $\vec{E} \times \vec{B}$ is in the direction in which the wave is propagating (the positive x-direction).
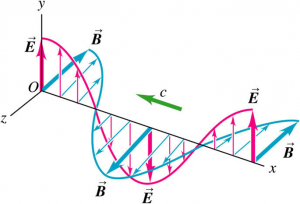
The figure above shows a linearly polarized sinusoidal electromagnetic wave travelling in the negative x-direction.
$$\begin{aligned} \vec{E}\left( x,t \right) =-E_{\text{max}} \cos{\left( kx + \omega t \right)}\hat{j} \\ \vec{B}\left( x,t \right) =-B_{\text{max}} \cos{\left( kx + \omega t \right)}\hat{k} \end{aligned}$$
The wave equation for electromagnetic waves in vacuum,
$$\begin{aligned} -\epsilon_{0}\mu_{0} \frac{\partial^{2} E_{y} \left( x,t \right)}{\partial t^{2}} + \frac{\partial^{2} E_{y} \left( x,t \right)}{\partial x^{2}} &= 0 \\ -\epsilon_{0}\mu_{0} \frac{\partial^{2} B_{z} \left( x,t \right)}{\partial t^{2}} + \frac{\partial^{2} B_{z} \left( x,t \right)}{\partial x^{2}} &= 0 \end{aligned}$$
Note: This is just a glimpse of the wave equation for electromagnetic waves. The electromagnetic wave equation will be dealt with more rigour in any Classical Electromagnetism textbooks or the Year 2/3 section of this website.
Next: Energy & Momentum In Electromagnetic Waves