In a region of empty space where $\vec{E}$ and $\vec{B}$ fields are present, the total energy density $u$ is given by:
$$u = \frac{1}{2} \epsilon_{0} E^{2} + \frac{1}{2 \mu_{0}} B^{2}$$
For electromagnetic waves in a vacuum,
$$\begin{aligned} B &= \frac{E}{c} \\ &= \sqrt{\epsilon_{0} \mu_{0}} E \end{aligned}$$
It follows that:
$$u = \epsilon_{0} E^{2}$$
In a vacuum, the energy density associated with the $\vec{E}$ field is equal to the energy of the $\vec{B}$ field.
In general, the energy density $u$ of an electromagnetic wave depends on position and time.
Electromagnetic waves transport energy from one region to another – they carry the energy density $u$ with them as they advance.
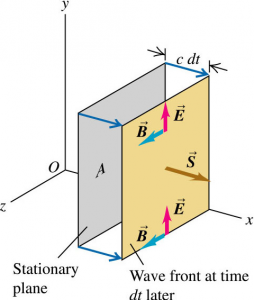
Consider a stationary plane, perpendicular to the x-axis, that coincides with the wave front at a certain time. In a time $dt$ after this, the wave front moves a distance $dx = c \, dt$ to the right of the plane.
Consider an area A on this stationary plane, the energy $dU$ in the space to the right of this area must have passed through the area to reach the new location.
Hence,
$$\begin{aligned} dU &= u \, dV \\ &= \left( \epsilon_{0} E^{2} \right) \left( Ac \, dt \right) \end{aligned}$$
The energy flow per unit time per unit area is given by:
$$\begin{aligned} S &= \frac{1}{A} \frac{dU}{dt} \\ &= \epsilon_{0} c E^{2} \\ &= \epsilon_{0} c^{2} E \left( \frac{1}{c} E \right) \\ &= \frac{1}{\mu_{0}} EB \end{aligned}$$
The energy flow per unit time per unit area has a term attached to it: Poynting vector, $\vec{S}$, where the direction is in the direction of propagation of the wave.
$$\begin{aligned} \vec{S} &= \frac{1}{\mu_{0}} \vec{E} \times \vec{B} \\ S &= \frac{1}{\mu_{0}} EB \end{aligned}$$
The total energy flow per unit time out of any closed surface is given by:
$$P = \oint \vec{S}.d\vec{A} $$
Let’s calculate the Poynting vector for typical sinusoidal waves:
$$\begin{aligned} \vec{E} \left( x,t \right) &= E_{\text{max}} \cos{\left( kx-\omega t \right)} \hat{j} \\ \vec{B} \left( x,t \right) &= B_{\text{max}} \cos{\left( kx-\omega t \right)} \hat{k} \end{aligned}$$
$$\begin{aligned} \vec{S} \left( x,t \right) &= \frac{1}{\mu_{0}} \vec{E}\left( x,t \right) \times \vec{B}\left( x,t \right) \\ &= \frac{1}{\mu_{0}} E_{\text{max}} B_{\text{max}} \cos^{2}{\left( kx-\omega t \right)} \hat{i} \\ &= \frac{1}{2 \mu_{0}} E_{\text{max}} B_{\text{max}} \left[ 1 + \cos{2 \left( kx-\omega t \right)} \right] \hat{i} \end{aligned}$$
The intensity of the radiation is the magnitude of the average value of the Poynting vector,
$$\begin{aligned} I &= S_{\text{average}} \\ &= \frac{E_{\text{max}} B_{\text{max}}}{2 \mu_{0}} \\ &= \frac{1}{2 \mu_{0} c} E_{\max}^{2} \\ &= \frac{c}{2 \mu_{0} c^{2}} E_{\text{max}}^{2} \\ &= \frac{1}{2} \epsilon_{0} c E_{\text{max}}^{2} \\ &= \frac{1}{2} \sqrt{\frac{\epsilon_{0}}{\mu_{0}}} E_{\text{max}}^{2} \end{aligned}$$
Electromagnetic waves also carry momentum $p$, with a corresponding momentum density. Let’s calculate the momentum carried by electromagnetic waves by using the well known relativistic formula: $E^{2} = p^{2}c^{2} + m^{2}c^{4}$. According to quantum mechanics, the electromagnetic radiation is made up of massless particles called photons, with momentum $p = \frac{E}{c}$ for individual photons.
It follows from $p = \frac{E}{c}$ that the momentum density for electromagnetic waves must be equal to the energy density divided by c. Since the energy density for electromagnetic waves is given by: $u = \epsilon_{0} E^{2}$
$$\begin{aligned} \frac{dp}{dV} &= \frac{\epsilon_{0} E^{2}}{c} \\ &= \epsilon_{0} EB \\ &= \frac{EB}{\mu_{0}c^{2}} \\ &= \frac{S}{c^{2}} \end{aligned}$$
We can further express the above as momentum transferred per unit time per unit area:
$$\begin{aligned} \frac{dp}{dV} &= \frac{S}{c^{2}} \\ \frac{dp}{Ac \, dt} &= \frac{S}{c^{2}} \\ \frac{1}{A} \frac{dp}{dt} &= \frac{S}{c} \\ \frac{1}{A} \frac{dp}{dt} &= \frac{EB}{\mu_{0}c} \end{aligned}$$
This momentum is a property of the field – it is not associated with the mass of a moving particle in the usual sense. This momentum is responsible for the phenomenon of radiation pressure. If an electromagnetic wave with an average value of Poynting vector of $S_{\text{av}}$ is incident on an object, with no reflection and transmission, the radiation pressure on the object will be given by: (NOTE: $p_{\text{rad}}$ is radiation pressure and $dp$ is the infinitesimal change in momentum.)
$$\begin{aligned} p_{\text{rad}} &= \frac{F_{\text{rad}}}{A} \\ &= \frac{1}{A} \frac{dp}{dt} \\ &= \frac{S_{\text{av}}}{c} \\ &= \frac{I}{c} \end{aligned}$$
If all of the incident electromagnetic waves are reflected by the object, the resulting radiation pressure will be:
$$\begin{aligned} p_{\text{rad}} &= \frac{2 S_{\text{av}}}{c} \\ &= \frac{2I}{c} \end{aligned}$$
Next: Standing Electromagnetic Waves
Previous: Electromagnetic Spectrum & Sinusoidal EM Plane Waves