The superposition principle holds for electromagnetic waves just as for electric and magnetic fields. Electromagnetic waves can be reflected off the surface of a conductor or a dielectric.
The superposition of an incident wave and a reflected wave forms a standing wave.
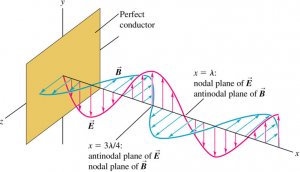
Suppose a sheet of a perfect conductor (zero resistivity) is placed in the yz-plane and a linearly polarized electromagnetic wave, travelling in the x-direction, strikes it.
$$\begin{aligned} E_{y} \left( x,t \right) &= E_{\text{max}} \left[ \cos{\left( kx + \omega t \right)}-\cos{\left( kx-\omega t \right)} \right] \\ &=-2 E_{\text{max}} \sin{kx} \sin{\omega t} \end{aligned}$$
From above, the magnitude of the electric field is zero (nodal planes) at:
$$x = 0, \frac{\lambda}{2}, \lambda, \frac{3 \lambda}{2}, \dots$$
$$\begin{aligned} B_{z} \left( x,t \right) &= B_{\text{max}} \left[-\cos{\left( kx + \omega t \right)}-\cos{\left( kx-\omega t \right)} \right] \\ &=-2 B_{\text{max}} \cos{kx} \cos{\omega t} \end{aligned}$$
From above, the magnitude of the magnetic field is zero (nodal planes) at:
$$x = \frac{\lambda}{4}, \frac{3 \lambda}{4}, \frac{5 \lambda}{4}, \dots$$
The nodes of $\vec{E}$ coincide with the antinodes of $\vec{B}$, and conversely.
Now, insert a second conducting plane, parallel to the first and a distance L from it, along the positive x axis.
Both conducting planes must be nodal planes for $\vec{E}$, i.e., a standing wave can exist only when the second plane is placed at one of the positions where $E \left( x, t \right) = 0$.
For a standing wave to exist, $L$ must be an integer multiple of $\frac{\lambda}{2}$.
The wavelengths that satisfy this condition are:
$$\begin{aligned} \lambda_{n} &= \frac{2L}{n} \, \, \, \left( n = 1, 2, 3, \dots \right) \\ f_{n} &= \frac{c}{\lambda_{n}} = n \frac{c}{2L} \, \, \, \left( n = 1, 2, 3, \dots \right) \end{aligned}$$
There is a set of normal modes, each with a characteristic frequency, wave shape, and node pattern.