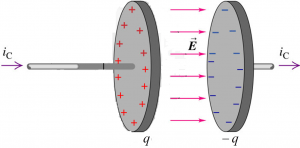
Consider the process of charging a parallel-plate capacitor.
Conducting wires lead (conduction) current $i_{C}$ into one plate and out of the other. The charge q increases, and the electric field between the plates increases.
Recall that: (for a parallel-plate capacitor)
$$\begin{aligned} q &= Cv \\ C &= \epsilon \frac{A}{d} \\ E &= \frac{v}{d} \end{aligned}$$
Let’s compute $i_{C}$,
$$\begin{aligned} i_{c} &= \frac{dq}{dt} \\ &= \frac{d}{dt} \left( Cv \right) \\ &= \frac{d}{dt} \left[ \left( \epsilon \frac{A}{d} \right) Ed \right] \\ &= \frac{d}{dt} \left( \epsilon EA \right) \\ &= \frac{d}{dt} \left( \epsilon \Phi_{E} \right) \\ &= \epsilon \frac{d \Phi_{E}}{dt} \end{aligned}$$
The equation above states that there is a current generated by a change in electric flux, and that current has the same magnitude as $i_{C}$. What is the identity of this mysterious current?
From Kirchhoff’s junction rule, the same current enters the left plate ($i_{C}$) as leaves the right plate. Although current is flowing through the capacitor, no actual charge is transported through the vacuum between its plates. The explanation is that a displacement current $i_{D}$ “flows” in the vacuum.
Hence, the mysterious current is:
$$i_{D} = \epsilon \frac{d \Phi_{E}}{dt}$$
Can we detect this current?
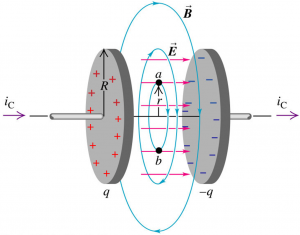
According to Ampere’s Law, a magnetic field should exists between the plate as it should be “generated” by the displacement current. Let’s find the magnetic field through a plane circular area of radius r (where $r \leq R$) by Ampere’s Law:
$$\begin{aligned} \oint \vec{B}.d\vec{l} &= \mu_{0} I \\ 2 \pi rB &= \mu_{0} \left( \frac{i_{D}}{\pi R^{2}} \times \pi r^{2} \right) \\ 2 \pi rB &= \mu_{0} i_{C} \frac{r^{2}}{R^{2}} \\ B &= \frac{\mu_{0}i_{C}}{2 \pi} \frac{r}{R^{2}} \end{aligned}$$
When r = R, we find that the magnetic field is:
$$B = \frac{\mu_{0} i_{C}}{2 \pi R}$$
Which is exactly the magnetic field generated by a long, straight conductor carrying a current $i_{C}$. If you measure the magnetic field at the gap of the capacitors, you will come to the conclusion that there is a current “flowing” through the gap of the capacitors.
Generalized Ampere’s Law
Consider the Ampere’s Law:
$$\oint \vec{B}.d\vec{l} = \mu_{0} \left( I \right)_{\text{encl}}$$
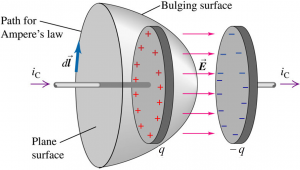
If the path is chosen as seen in the figure above, but the surface is chosen to be a plane perpendicular to the wire (not curved) and enclosing $i_{C}$. Ampere’s Law will give:
$$\oint \vec{B}.d\vec{l} = \mu_{0} \left( i_{C} \right)_{\text{encl}}$$
Recall that the surface can be arbitrarily chosen (the results will NOT change). Hence, if the area bounded by the integration path is chosen as shown above, the current enclosed by the area bounded by the integration path will be $i_{D}$ (from the conclusion above). We will obtain:
$$\oint \vec{B}.d\vec{l} = \mu_{0} \left( i_{D} \right)_{\text{encl}}$$
, which is equals to $\oint \vec{B}.d\vec{l} = \mu_{0} \left( i_{C} \right)_{\text{encl}}$. (as $i_{C} = i_{D}$)
IF you deny the existence of the displacement current, you will obtain:
$$\oint \vec{B}.d\vec{l} = 0$$
, which is not correct.
Armed with the knowledge that the displacement current is “real”, we would need to modify the Ampere’s Law to take into account of the displacement current.
Consider a situation where there is a real current ($i_{C}$) and a displacement current ($i_{D}$) enclosed in the area bounded by the integration path:
$$\begin{aligned} \oint \vec{B}.d\vec{l} &= \mu_{0} \left( i_{C} + i_{D} \right)_{\text{encl}} \\ \oint \vec{B}.d\vec{l} &= \mu_{0} \left( i_{C} + \epsilon \frac{d \Phi_{E}}{dt} \right)_{\text{encl}} \end{aligned}$$
The above equation states that a varying electric field gives rise to a magnetic field.
Previous: Induced Electric Field
Back To Electromagnetism (UY1)